a: Xét ΔANH vuông tại N và ΔAHC vuông tại H có

góc NAH chung

Do đó: ΔANH\(\sim\)ΔAHC

b: \(HC=\sqrt{15^2-12^2}=9\left(cm\right)\)

c: Xét ΔAHB vuông tại H có HM là đường cao

nên \(AM\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HN là đường cao

nên \(AN\cdot AC=AH^2\left(2\right)\)

Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

refer

a: Xét ΔAEM vuông tại M và ΔAHM vuông tại M có

AM chung

ME=MH

Do đó: ΔAEM=ΔAHM

b: Xét ΔBHE có 

BM là đường cao

BM là đường trung tuyến

Do đó: ΔBHE cân tại B

Xét ΔAEB và ΔAHB có 

AE=AH

EB=HB

AB chung

Do đó: ΔAEB=ΔAHB

Suy ra: ˆAEB=ˆAHB=900AEB^=AHB^=900

hay AE⊥EB

tham khảo

a: Xét ΔAEM vuông tại M và ΔAHM vuông tại M có

AM chung

ME=MH

Do đó: ΔAEM=ΔAHM

b: Xét ΔBHE có 

BM là đường cao

BM là đường trung tuyến

Do đó: ΔBHE cân tại B

Xét ΔAEB và ΔAHB có 

AE=AH

EB=HB

AB chung

Do đó: ΔAEB=ΔAHB

Suy ra: ˆAEB=ˆAHB=900AEB^=AHB^=900

hay AE⊥EB

Câu 1:
Xét tam giác ABH vuông tại H, ta có:
   AB² = AH² +  HB² (định lý Py-ta-go)
   20²  = AH² + 16²
   400  = AH² + 256
   AH² = 400 - 256
   AH² = 144
   AH  = \(\sqrt{144}\)= 12 (cm)

Xét tam giác AHC vuông tại H, ta có:
   AC² = AH² + HC² (định lý Py-ta-go)
   AC² = 12²  + 5²
   AC² = 144  + 25
   AC² = 169
   AC  = \(\sqrt{169}\)= 13 (cm)

Vậy AH = 12 cm
       AC = 13 cm

Bài 2:
Xét tam giác AHC vuông tại H, ta có:
   AC² = AH² + HC² (định lý Py-ta-go)
   15²  = AH² + 9²
   225  = AH² + 81
   AH² = 225 - 81
   AH² = 144
   AH  = \(\sqrt{144}\)= 12 (cm)

Xét tam giác AHB vuông tại, ta có:
   AB² = AH² + HB² (định lý Py-ta-go)
   AB² = 12²  + 5²
   AB² = 144  + 25
   AB² = 169
   AB  = \(\sqrt{169}\)= 13 (cm)

Vậy AB = 13 cm

Câu này dễ

AH 12cm

AC13cm

AB13cm

a, Vẽ tia HM là tia đối của tia AH , sao cho BH =HC

Xét tg AHB và AHC 

Có : H là góc chung

BH=HC

AH=HM

Vậy : tg AHB= tg AHC

Nên : MC=AB ( tg AHB = tg AHC)

Có : AM < AC+CM (bdt)

Mà :  AM=2AH và AC+CM=AC+AB

Nên : 2AH=AC+AB

=> AH=AC+B/2

Vậy đpcm ở câu a

b, từ rồi mk lm

Nên :2AH<AC+AB

=> AH=AC+AB/2

Vậy đpcm ở câu a

Áp dụng định lí Py-ta-go vào tam giác ABH vuông tại H, ta có:

AH²+BH²=AB²

AH²=AB²−BH²

AH²=52−32

⇒AH²=16

⇒AH=4(cm)

Ta có:

BH+HC=BC

⇒HC=BC−BH

⇒HC=8−3

⇒HC=5(cm)

Áp dụng định lí Py-ta-go vào tam giác AHC vuông tại H, ta có:

AH²+HC²=AC²

42+52=AC²

⇒AC²=41

⇒AC=√41(cm)

Vậy HC = 5 cm, AC = √41 cm

#Tuyên#

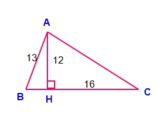
Áp dụng định lí Pi-ta-go trong ΔAHC vuông tại H ta có:

AC2 = AH2 + HC2 = 122 + 162 = 144 + 256 = 400

⇒ AC = 20 (cm)

Áp dụng định lí Pi-ta-go trong ΔAHB vuông tại H ta có:

BH2 + AH2 = AB2 ⇒ BH2 = AB2 - AH2 = 132 - 122 = 169 -144 = 25

⇒ BH = 5cm

Do đó BC = BH + HC = 5 + 16 = 21 (cm)

ta có:

\(BH^2=AB^2-AH^2=13^2-5^2=169-25=144\)

\(BH=\sqrt{144}=12\)

\(HC^2=AC^2-AH^2=9^2-5^2=81-25=56\)

\(HC=\sqrt{56}\)

BC=BH+HC=căn 56 +12

  tam giác AHB vuông tại H có: BH²=AB²-AH²=13²-12²=25( ĐL Pytago) => BH=5 cm

BC=BH+HC=5+16=21 cm

Tam giác AHC vuông tại H có: AH²+ HC²=AC²( đl Pytago) --> AC²=12²+ 16²=20 cm

Tam giác AHB vuông tại H có: AB²= AH²+BH²( đli Pytago)  => BH²=AB²-AH²=13²- 12²=25 -> BH=5 cm

BC= BH+HC=5+16=21 cm

Tam giác AHC vuông tại H có: AC²= AH²+HC²( đli Pytago) => AC²= 12²+ 16²=400 --> AC= 20 cm

Áp dụng Py-ta-go vào \(\Delta\) vuông AHC ta có:

AC² = AH² + HC²

hay AC² = 12² + 16²

=> AC² = 400

=> AC = 20 cm

Áp dụng Py-ta-go vào \(\Delta\) vuông AHC ta có:

AB² = AH² + BH²

hay 13² = 12² + BH²

=> BH² = 13² - 12²

=> BH² = 25

=> BH = 5 cm

Có BC = BH + HC

hay BC = 5 + 16 = 21

Vậy AC = 20 cm và BC = 21cm

XONG !!