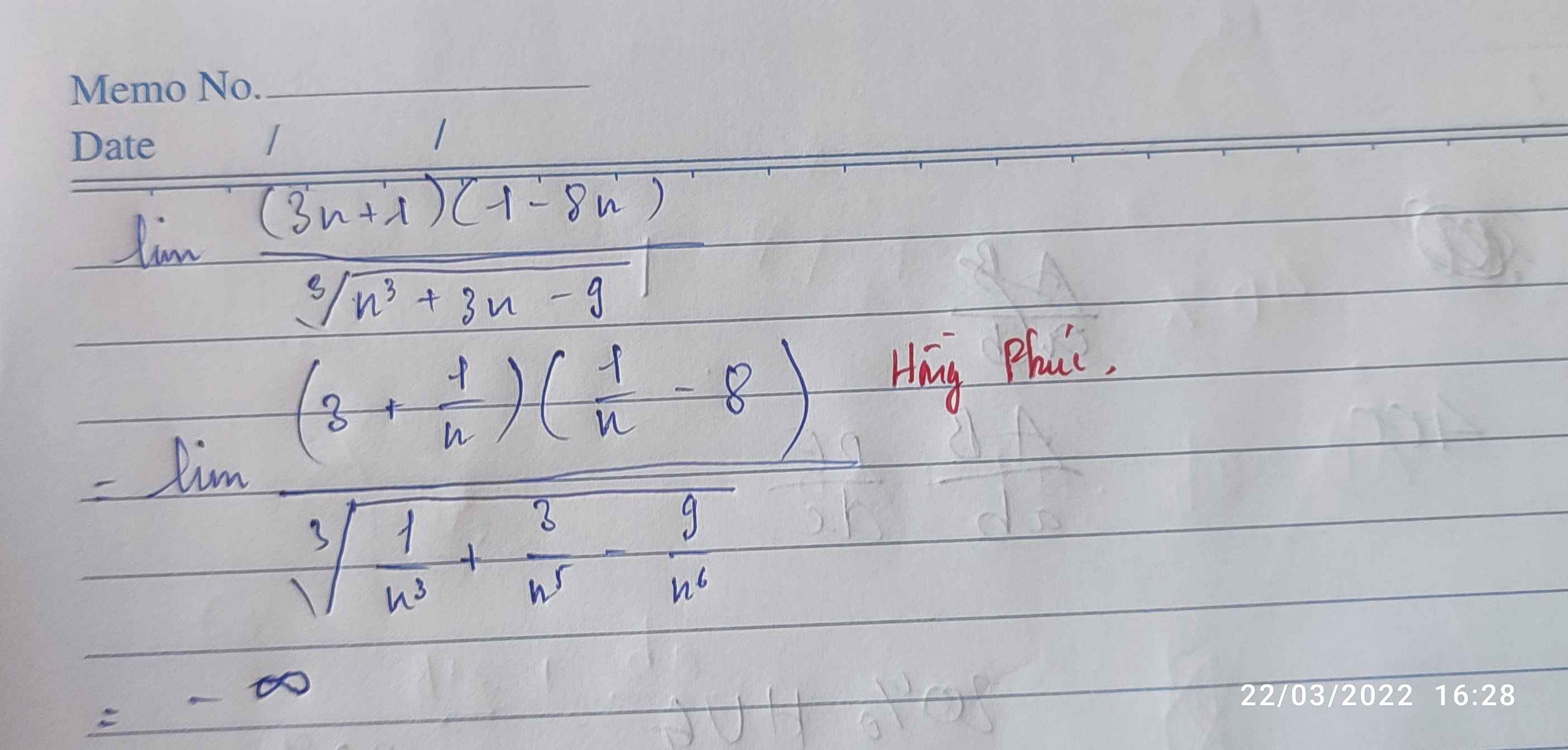B = 3 + 3 ² + 3 ³ + ... + 3 ¹⁹⁹²

B = ( 3 + 3 ² + 3 ³ ) + ... + ( 3 ¹⁹⁹⁰ + 3 ¹⁹⁹¹ + 3 ¹⁹⁹² )

B = ( 3 + 3 ² + 3 ³ ) + ... +( 3 + 3 ² + 3 ³ ) . 3 ¹⁹⁸⁹

B = 39 + ... + 39 . 3 ¹⁹⁸⁹

B = 39 ( 1 + ... + 3 ¹⁹⁸⁹ )

Vì 39 chia hết cho 13

=> B chia hết cho 13

B = 3 + 3 ² + 3 ³ + ... + 3 ¹⁹⁹²

B = ( 3 + 3 ² + 3 ³ + 3 ⁴ ) + ... + ( 3 ¹⁹⁸⁹ + 3 ¹⁹⁹⁰ + 3 ¹⁹⁹¹ + 3 ¹⁹⁹²  )

B = ( 3 + 3 ² + 3 ³ + 3 ⁴ ) + ... + ( 3 + 3 ² + 3 ³ + 3 ⁴ ) . 3 ¹⁹⁸⁸

B = 120 + ... + 120 . 3 ¹⁹⁸⁸

B = 120 ( 1 + ... + 3 ¹⁹⁸⁸ )

Vì 120 chia hết cho 40

=> B chia hết cho 40

b) \(\Rightarrow\left(n+2\right)\inƯ\left(19\right)=\left\{-19;-1;1;19\right\}\)

Do \(n\in N\)

\(\Rightarrow n\in\left\{17\right\}\)

a) Do \(n\in N\)

\(\Rightarrow n\inƯ\left(15\right)=\left\{1;3;5;15\right\}\)

c) \(\Rightarrow\left(n+1\right)+8⋮\left(n+1\right)\)

Do \(n\in N\Rightarrow n\inƯ\left(8\right)=\left\{1;2;4;8\right\}\)

d) \(\Rightarrow3\left(n+1\right)+18⋮\left(n+1\right)\)

Do \(n\in N\Rightarrow\left(n+1\right)\inƯ\left(18\right)=\left\{1;2;3;6;9;18\right\}\)

\(\Rightarrow n\in\left\{0;1;2;5;8;17\right\}\)

e) \(\Rightarrow\left(n-2\right)+10⋮\left(n-2\right)\)

Do \(n\in N\Rightarrow\left(n-2\right)\inƯ\left(10\right)=\left\{-2;-1;1;2;5;10\right\}\)

\(\Rightarrow n\in\left\{0;1;3;4;7;12\right\}\)

f) \(\Rightarrow n\left(n+4\right)+11⋮\left(n+4\right)\)

Do \(n\in N\Rightarrow\left(n+4\right)\inƯ\left(11\right)=\left\{11\right\}\)

\(\Rightarrow n\in\left\{7\right\}\)

 \(19:\left(n+2\right)\)

⇒ (n+2)∈Ư(19)=(1,19)

n+2            1               19

n               -1(L)           17(TM)

Giải

\(3n+9=3\left(n+3\right)=3\left(n-2+5\right)=3.\left(n-2\right)+15⋮n-2\\ \Leftrightarrow n-2\inƯ\left(15\right)\\ Ư\left(15\right)=\left\{1;-1;3;-3;5;-5;15;-15\right\}\\ =>n=\left\{3;1;5;-1;7;-3;17;-13\right\}\)

Vậy \(n=\left\{1;3;5;-1;7;-3;17;-13\right\}\)

Từ đề bài suy ra 3⁴ > 3^{n ≥}  3², tìm được n ∈ {2; 3}

a) \(\frac{1}{9.27n}=3n\)

=> \(\frac{1}{3^5n}=3n\)

=> \(\frac{1}{n}3^{-5}=3n\)

=> \(\frac{1}{n}:n=3:3^{-5}\)

=> \(n^{-2}=3^{-4}=9^{-2}\)

Vậy n=9

Lời giải:
Để $\frac{3n+9}{n-4}$ là số hữu tỉ dương thì có 2 TH xảy ra:

TH1: 

\(\left\{\begin{matrix} 3n+9>0\\ n-4>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} n>-3\\ n>4\end{matrix}\right.\Leftrightarrow n>4\)

TH2: 

\(\left\{\begin{matrix} 3n+9< 0\\ n-4< 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} n< -3\\ n< 4\end{matrix}\right.\Leftrightarrow n< -3\)