Cho hàm số
y = f(x) = (4 - m^2)x^2 - (2m + 1)x+3
Tìm m để hàm số luôn đồng biến trên tập số thực R
Cho hàm sốy = f(x). Hàm số y = f’(x) có đồ thị như hình bên. Hàm số y = f(2-x) đồng biến trên khoảng
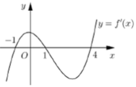
A. (1;3).
B. (2;+∞).
C. (-2;1).
D. (-∞;-2).
Cho hàm số bậc nhất y=f(x)=(m^2+m+1)x+5.Chứng minh rằng:hàm số luôn đồng biến trên R
`a=m^2+m+1=m^2+2.m. 1/2 + (1/2)^2 + 3/4= (m+1/2)^2 + 3/4 >0 forall m`
`=> a>0 =>` Hàm số luôn đồng biến trên `RR`.
Để hàm số trên đồng biến khi \(m^2+m+1=m^2+m+\dfrac{1}{4}+\dfrac{3}{4}=\left(m+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
Vậy hàm số luôn đồng biến trên R
Ta có: \(m^2+m+1\)
\(=m^2+2\cdot m\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(m+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall m\)
Do đó: Hàm số \(f\left(x\right)=\left(m^2+m+1\right)x+5\) luôn đồng biến trên R
Câu 5. Cho hàm số f x có đạo hàm liên tục tên R và có đạo hàm ' 2 f x x x 9 1 .Tìm m để hàm số 2 y f x x m 2 đồng biến trên 1,3
y=(2m-1)x+m-7
a,tìm m để hàm số đồng biến trên R
b, tìm điểm cố định mà hàm số luôn đi qua với mọi m
a)HS đồng biến
`=>2m-1>0`
`=>2m>1=>m>1/2`
b)Gọi điểm cố đính mà hàm số luôn đi qua với mọi m là `A(x_o,y_o)`
`=>y_o=(2m-1).x_o +m-7`
`<=>y_o=2mx_o-x_o +m-7`
`<=>m(2x_o +1)-x_o-y_o-7=0`
`<=>{(2x_o +1=0),(-x_o-y_o-7=0):}`
`<=>x_o=-1/2,y_o=-13/2`
`=>A(-1/2,-13/2)`
Vậy điểm cố đính mà hàm số luôn đi qua với mọi m là `A(-1/2,-13/2)`
a: Để hàm số đồng biến thì 2m-1>0
hay \(m>\dfrac{1}{2}\)
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x ( x - 2 ) 2 ( 2 x + m + 1 ) với mọi x ∈ R . Có bao nhiêu số nguyên âm m để hàm số g ( x ) = f ( x 2 ) đồng biến trên khoảng ?
A. 5.
B. 2.
C. 3.
D. 4.
Cho hàm số y=(m2-2m+3)x-4 (d) ,(với m là tham số)
1.Chứng minh rằng với mọi hàm số luôn đồng biến trên tập xác định của nó.
2.Tìm m để (d) đi qua A(2;8)
3.Tìm m để (d) song song với đường thẳng (d'):y=3x +m-4
2) Để (d) đi qua A(2;8) thì Thay x=2 và y=8 vào hàm số \(y=\left(m^2-2m+3\right)x-4\), ta được:
\(\left(m^2-2m+3\right)\cdot2-4=8\)
\(\Leftrightarrow2m^2-4m+6-4-8=0\)
\(\Leftrightarrow2m^2-4m-6=0\)
\(\Leftrightarrow2m^2-6m+2m-6=0\)
\(\Leftrightarrow2m\left(m-3\right)+2\left(m-3\right)=0\)
\(\Leftrightarrow\left(m-3\right)\left(2m+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m-3=0\\2m+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=3\\2m=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=3\\m=-1\end{matrix}\right.\)
Vậy: Để (d) đi qua A(2;8) thì \(m\in\left\{3;-1\right\}\)
3. Cho hàm số y = x^2- m^2+2m +1 /x -m . Tìm tập hợp các giá trị của tham số m để hàm số đồng biến trên khoảng xác định của nó?
\(y=\dfrac{x^2-m^2+2m+1}{x-m}\) đúng không nhỉ?
\(y'=\dfrac{x^2-2mx+m^2-2m-1}{\left(x-m\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi và chỉ khi:
\(x^2-2mx+m^2-2m-1\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=m^2-\left(m^2-2m-1\right)\le0\)
\(\Leftrightarrow m\le-\dfrac{1}{2}\)
Bài 11. Chứng minh rằng các hàm số sau đây luôn đồng biến với mọi số thực m ?
a: \(f\left(x\right)=\left(m^2+1\right)x+2m+1\)
b: \(f\left(x\right)=\dfrac{mx-1}{x+m}\)
Cho hàm số y=(m2 -2m+3)x - 4 (d)
chứng minh rằng với mọi m hàm số luôn đồng biến trên tập xác định của nó