Cầu lông có cầu thiết bị nào không vậy các bạn?

Những câu hỏi liên quan
lớp 6b có 22 bạn thích cầu lông có 23 bạn thích đá cầu có 21 bạn thích bóng bàn có 16 bạn thích cầu lông và đá cầu có 15 bạn thích đá cầu và bóng bàn có 17 bạn thích cầu lông và bóng bàn có 12 bạn thích cả 3 môn và có 3 bạn không thích môn nào hồi lớp 6b có bao nhiêu bạn
Lớp 10A có 24 bạn tham gia thi đấu bóng đá và cầu lông, trong đó có 16 bạn thi đấu bóng đá và 11 bạn thi đấu cầu lông. Giả sử các trận bóng đá và cầu lông không tổ chức đồng thời. Hỏi có bao nhiêu bạn lớp 10A tham gia thi đấu cả bóng đá và cầu lông?
Tham khảo:
Gọi \(x\) là số bạn tham gia thi đấu cả bóng đá và cầu lông.
Ta có: 16 bạn thi đấu bóng đá và 11 bạn thi đấu cầu lông
\( \Rightarrow \) Có \(16 - x\) bạn chỉ tham gia thi đấu bóng đá mà không thi đấu cầu lông.
Và có \(11 - x\) bạn chỉ tham gia thi đấu cầu lông mà không thi đấu bóng đá.
Ta có biểu đồ Ven như sau:
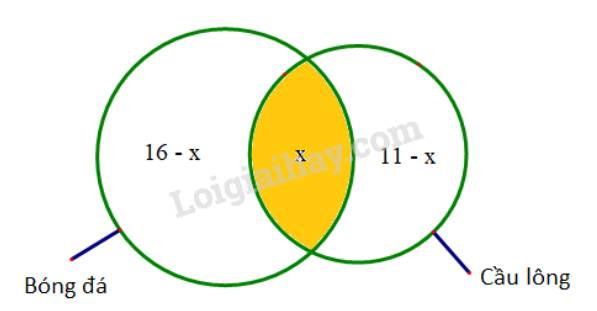
Tổng số bạn tham gia thi đấu bóng đá và cầu lông là: 16-x + x + 11-x = 24 => x=3.
Vậy lớp 10A có 3 bạn tham ggia thi đấu cả bóng đá và cầu lông.
Đúng 0
Bình luận (0)
gương cầu lõm dùng làm thiết bị nung nóng đúng không các bạn
Tham khảo:
Trong các ứng dụng trên, ứng dụng của gương cầu lõm là dùng làm thiết bị nung nóng. Vì: ... Theo tính chất của gương cầu lõm: Chùm tia phản xạ sẽ hội tụ tại một điểm trước gương, như vậy sức nóng của ánh sáng mặt trời nhờ gương cầu lõm đã được tập trung lại tại một điểm hội tụ
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Trong các trường hợp sau trường hợp nào không có cơ năng
A.Quả bóng nằm yên trên mặt đất
B.Lò xo bị kéo dãn
C.Sách nằm trên giá
D.Quả cầu lông đang bay
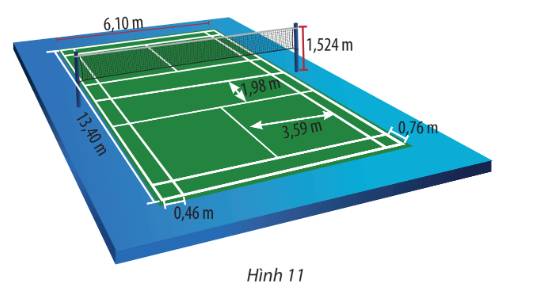
Trong bài toán ứng dụng, khi chơi trên sân cầu lông đơn, các lần phát cầu với thông tin như sau có được xem là hợp lệ không? (Các thông tin không được đề cập thì vẫn giữ như trong giả thiết bài toán trên)a) Vận tốc xuất phát của cầu là 12 m/sb) Vị trí phát cầu cách mặt đất 1,3 m.Lưu ý: Các thông số về sân cầu lông đơn được cho trong Hình 11.
Đọc tiếp
Trong bài toán ứng dụng, khi chơi trên sân cầu lông đơn, các lần phát cầu với thông tin như sau có được xem là hợp lệ không? (Các thông tin không được đề cập thì vẫn giữ như trong giả thiết bài toán trên)
a) Vận tốc xuất phát của cầu là 12 m/s
b) Vị trí phát cầu cách mặt đất 1,3 m.
Lưu ý: Các thông số về sân cầu lông đơn được cho trong Hình 11.
a)
Chọn hệ trục tọa độ như Hình 9 (vị trí rơi của cầu thuộc trục hoành và vị trí cầu rời mặt vợt thuộc trục tung).
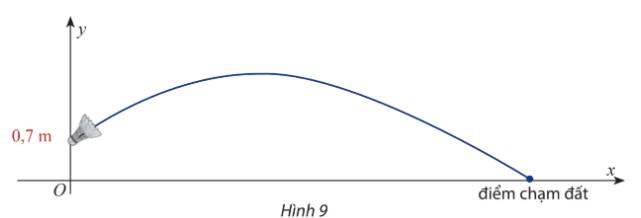
Với \(g = 9,8\;m/{s^2}\), góc phát cầu \(\alpha = {30^o}\), vận tốc ban đầu \({v_0} = 12\;m/s\), phương trình quỹ đạo của cầu là:
\(y = \frac{{ - 9,8}}{{{{2.12}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7 = - \frac{{4,9}}{{108}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7\)
Vị trí cầu rơi chạm đất là giao điểm của parabol và trục hoành nên giải phương trình \( - \frac{{4,9}}{{108}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7 = 0\) ta được \({x_1} \approx - 1,11\) và \({x_2} \approx 13,84\)
Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 13,84 m > 13,4 m (chiều dài cả sân)
Vậy lần phát cầu đã bị hỏng vì điểm rơi của cầu nằm ngoài đường biên ngoài.
b)
Ta so sánh tung độ của điểm trên quỹ đạo (có hoành động bằng khoảng cách từ điểm phát cầu đến chân lưới phân cách) với chiều cao mép trên của lưới.
Với \(g = 9,8\;m/{s^2}\), góc phát cầu \(\alpha = {30^o}\), vận tốc ban đầu \({v_0} = 8\;m/s\), vị trí phát cầu cách mặt đất 1,3 m. Phương trình quỹ đạo của cầu là:
\(y = \frac{{ - 9,8}}{{{{2.8}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3 = - \frac{{4,9}}{{48}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3\)
Khi \(x = 4,\)ta có \(y = - \frac{{4,9}}{{48}}{.4^2} + \frac{{\sqrt 3 }}{3}.4 + 1,3 \approx 1,98 > 1,524\)
Vậy quỹ đạo của cầu cao hơn mép trên của lưới.
Tiếp theo ta kiểm tra vị trí cầu rơi có vượt đường biên ngoài hoặc chưa tới đường biên trong hay không.
Vị trí cầu rơi chạm đất là giao điểm của parabol và trục hoành nên giải phương trình \(y = \frac{{ - 9,8}}{{{{2.8}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3 = - \frac{{4,9}}{{48}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3\) ta được \({x_1} \approx - 1,73\) và \({x_2} \approx 7,38\)
Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 7.38 m.
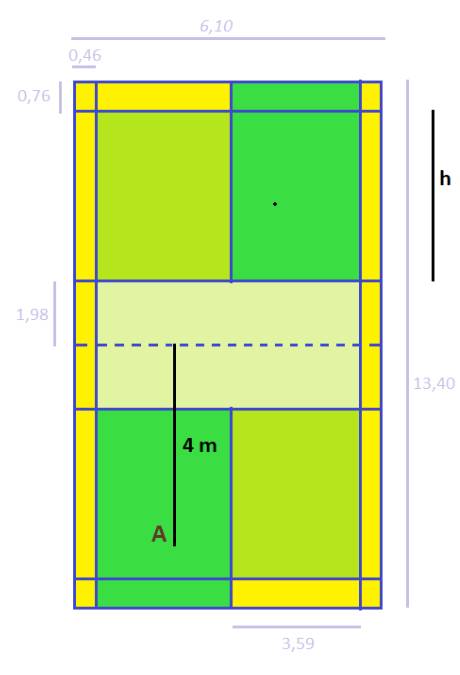
Dễ thấy: độ dài h (chiều dài của khu vực hợp lệ) là: \(13,4:2 - 1,98 -0,76= 3,96\) (m).
Do đó lần phát là hợp lệ nếu khoảng cách từ vị trí phát đến điểm rơi thuộc khoảng \(4 + 1,98 = 5,98(m)\) và \(4 + 1,98 +3,96= 9,94(m)\) và \(5,98 < 7,38 < 9,94\).
Như vậy vị trí quả cầu trên mặt đất nằm giữa đường biên trong và đường biên ngoài.
Kết luận: lần phát cầu này được coi là hợp lệ.
Đúng 0
Bình luận (0)
một lớp học có 50 học sinh được đăng kí chơi 2 môn thể thao. cầu lông. bóng bàn. Có 30 bạn đăng kí chơi cầu lông. 28 bạn chơi bóng bàn và 10 bạn không chơi môn nào. Hỏi có bao nhiêu bạn đăng kí chơi 2 môn và 1 môn Toán 10
Gọi \(A,B\) lần lượt là tập hợp các học sinh đăng kí chơi cầu lông và chơi bóng bàn.
Như vậy tập hợp học sinh đăng kí chơi cả hai môn là \(A\cap B\). Tập hợp học sinh đăng kí ít nhất một môn là \(A\cup B\)
Ta có \(N\left(A\cup B\right)=N\left(A\right)+N\left(B\right)-N\left(A\cap B\right)\)
\(18\) học sinh đăng kí chơi cả hai môn
\(b,\) Số học sinh chỉ đăng kí chơi một môn là
Đúng 2
Bình luận (0)
Câu 1: Thiết bị nào sau đây là thiết bị bảo vệ A. Công tắc B. Ổ cắm C. Cầu daoD. Cầu chìCâu 2: Để kiểm tra mạng điện có điện hay không người ta dùng dụng cụ gìA. Kìm điệnB. Bút thử điện C. Tua vít D. Đồng hồ vạn năngCâu 3. Yêu cầu nào là quan trọng nhất khi thiết kế mạng điện trong nhàA. Đảm bảo tính kinh tếB. Đảm bảo tính thẩm mĩC. Đảm bảo an toàn điệnD. Dễ dàng kiểm tra, sửa chữaCâu 4. Vì sao cầu chì luôn phải mắc ở dây phaA. Để ngắt được mạch điện khi có sự cốB. Để thuận...
Đọc tiếp
Câu 1: Thiết bị nào sau đây là thiết bị bảo vệ
A. Công tắc
B. Ổ cắm
C. Cầu dao
D. Cầu chì
Câu 2: Để kiểm tra mạng điện có điện hay không người ta dùng dụng cụ gì
A. Kìm điện
B. Bút thử điện
C. Tua vít
D. Đồng hồ vạn năng
Câu 3. Yêu cầu nào là quan trọng nhất khi thiết kế mạng điện trong nhà
A. Đảm bảo tính kinh tế
B. Đảm bảo tính thẩm mĩ
C. Đảm bảo an toàn điện
D. Dễ dàng kiểm tra, sửa chữa
Câu 4. Vì sao cầu chì luôn phải mắc ở dây pha
A. Để ngắt được mạch điện khi có sự cố
B. Để thuận tiện khi lắp đặt
C. Để đảm bảo tính thẩm mĩ
D. Để dễ dàng kiểm tra sửa chữa
Câu 5. Trên dây dẫn điện ghi VCm- 2,5 nghĩa là
A. Dây đồng mềm 1 lõi tiết diện lõi 2,5
B. Dây đồng mềm 2 lõi tiết diện lõi 2,5
C. Dây nhôm mềm 1 lõi, tiết diện lõi 2,5
D. Dây nhôm mềm 2 lõi, tiết diện lõi 2,5
mình đố cách bạn nè:1.Trong lớp có 50 học sinh trong đó có 30 học sinh tham gia chơi cầu lông. 25 học sinh chơi bóng bàn. Còn 7 học sinh không chơi cầu lông, không chơi bóng bàn. Hỏi có mấy học sinh vừa chơi cầu lông vừa chơi bóng bàn.2. Trong một phép chia hai số tự nhiên biết thương bằng 3 và số dư bằng 24, hiệu giữa số bị chia và số chia bằng 218. Tìm số bị chia và số chia.giúp mình nha!!!!
Đọc tiếp
mình đố cách bạn nè:
1.Trong lớp có 50 học sinh trong đó có 30 học sinh tham gia chơi cầu lông. 25 học sinh chơi bóng bàn. Còn 7 học sinh không chơi cầu lông, không chơi bóng bàn. Hỏi có mấy học sinh vừa chơi cầu lông vừa chơi bóng bàn.
2. Trong một phép chia hai số tự nhiên biết thương bằng 3 và số dư bằng 24, hiệu giữa số bị chia và số chia bằng 218. Tìm số bị chia và số chia.
giúp mình nha!!!!
C1: Số h/s tham gia hai môn là:
( 30 +25 +7 ) - 50 = 12 (h/s)
C2: SỐ H/S THAM GIA HAI MÔN LÀ:
50 - 7 = 43 (H/S)
SỐ HỌC SINH VỪA CHƠI CẦU LÔNG VỪA CHƠI BÓNG BÀN LÀ:
(30+25)-43= 12 (H/S)
2. TA CÓ SƠ ĐỒ:
SỐ BÉ !____!
218
SỐ LỚN !____!____!____!_24___!
SỐ CHIA LÀ:
(218-24) : (3+1)= 97
SỐ BỊ CHIA LÀ:
218 -97= 121
Đúng 0
Bình luận (0)
Ngoài giờ học, ngày nào Linh cũng tham gia các hoạt động: đánh cầu lông, đánh đàn và bơi. Trong 30 ngày gần đây, chỉ có 1 ngày Linh đã tham gia đủ cả ba hoạt động. Biết rằng Linh chơi cầu lông trong 19 ngày, tập bơi trong 12 ngày và đánh đàn trong 5 ngày. Có 1 ngày Linh chơi cầu lông và đánh đàn mà không đi bơi. Có 2 ngày Linh đi bơi và đi đánh cầu lông nhưng không đánh đàn. Hỏi có bao nhiêu ngay Linh đi đánh đàn và đi bơi mà không đi chơi cầu lông?
Đọc tiếp
Ngoài giờ học, ngày nào Linh cũng tham gia các hoạt động: đánh cầu lông, đánh đàn và bơi. Trong 30 ngày gần đây, chỉ có 1 ngày Linh đã tham gia đủ cả ba hoạt động. Biết rằng Linh chơi cầu lông trong 19 ngày, tập bơi trong 12 ngày và đánh đàn trong 5 ngày. Có 1 ngày Linh chơi cầu lông và đánh đàn mà không đi bơi. Có 2 ngày Linh đi bơi và đi đánh cầu lông nhưng không đánh đàn. Hỏi có bao nhiêu ngay Linh đi đánh đàn và đi bơi mà không đi chơi cầu lông?
























