Tính chu vi và diện tích tam giác ABC biết A(0;4); B(3;2); và C(2;0)
Cho tam giác ABC. Cho biết chu vi và diện tích của tam giác ABC thứ tư là P và S. Tính chu vi và diện tích tam giác AMN.
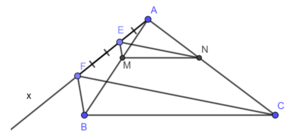
* Cách vẽ:
- Kẻ tỉa Ax bất kì khác tia AB, AC
- Trên tia Ax, lấy hai điểm E và F sao cho AE = 2 (đơn vị dài), EF = 3 (đơn vị dài)
- Kẻ đường thẳng FB
- Từ E kẻ đường thẳng song song với FB Cắt AB tại M.
- Kẻ đường thẳng FC.
- Từ E kẻ đường thẳng song song với FC cắt AC tại N.
Ta có M, N là hai điểm cần vẽ.
* Chứng minh:
Gọi p' và S' là chu vi và diện tích của △ AMN.
Trong △ ABC, ta có: MN // BC
Suy ra: △ AMN đồng dạng ΔABC
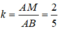
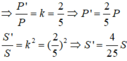
Cho tam giác ABC vuông tại A đcao AH biết AB=6cm và diện tích tam giác ABC=24cm2 Tính chu vi tam giác AHC
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\)
=>1/2*6*AC=24
=>AC*3=24
=>AC=8cm
=>BC=10cm
AH=6*8/10=4,8cm
H=8^2/10=6,4cm
S AHC=1/2*4,8*6,4=15,36cm2
Bài 1: hình chữ nhật có chiều dài 12cm, chiều rộng 8cm. Tính chu vi và diện tích HCN
bài 2: chu vi hcn bằng chu vi hình vuông cạnh 20cm. chiều dài hcn bằng 25cm. Tính diện tích hcn
bài 3: cho tam giác ABC có diện tích bằng 120cm2. Biết chiều cao AH =10cm . Tính độ dài cạnh BC.
Bài 4: cho tam giác ABC, AH là đường cao của tam giác ABC. biết AH =5cm, BC =8cm. Tính diện tích tam giác ABC.
Bài 1 Giải
Chu vi HCN là:
(12+8).2= 40(cm)
Diện tích HCN là:
12.8= 96(cm)
Bài 2 Chu vi hình vuông là:
20.4=80(cm)
Mà chu vi hình vuông bằng chu vi HCN nên:
Chiều rộng HCN là:
(80:2) -25=15(cm)
Diện tích HCN là:
15.25=375(cm)
Bài 3 Độ dài cạnh BC là:
120:10.2=24(cm)
Bài 4 Diện tích tam giác ABC là:
( 5.8):2 = 20(cm)
Chúc bn hok tốt~~
cho tam giác ABC ~tam giác MNP với tỉ sốk=1/3
a,tính tỉ số:2 chu vi,2 diện tích,2 đường cao tương ứng.
b,hiệu chu vi 2 tam giác là 60cm.tính chu vi mỗi tam giác.
c,biết tổng 2 diện tích tam giác là 640cm2.tính diện tích mỗi tam giác
a. Ta có: ▲ABC∼▲MNP (gt)
=>\(\dfrac{P_{ABC}}{P_{MNP}}=\dfrac{AH}{MQ}=k=\dfrac{1}{3}\) (với AH,MQ lần lượt là đường cao của tam giác ABC, MNP)
\(\dfrac{S_{ABC}}{S_{MNP}}=k^2=\dfrac{1}{9}\)
b. Ta có: \(\dfrac{P_{ABC}}{P_{MNP}}=\dfrac{1}{3}\)(cmt)=>PMNP=3PABC
*PMNP-PABC=60cm
=>3PABC-PABC=60cm
=>2PABC=60cm
=>PABC=30cm ; PMNP=90cm
c. Ta có: \(\dfrac{S_{ABC}}{S_{MNP}}=\dfrac{1}{9}\)(cmt)=>SMNP=9SABC
*SMNP+SABC=640cm2
=>9SABC+SABC=640cm2
=>10SABC=640cm2
=>SABC=64cm2 ; SMNP=576cm2
Cho ∆ABC~∆MNP với tỉ số k=1/3
a)tính tỉ số 2 chu vi,2 diện tích,2 đường cao tương ứng
b)hiệu chu vi 2 tam giác=60cm.Tính chu vi mỗi tam giác
c)biết tổng 2 diện tích tam giác là 640cm2.Tính diện tích mỗi tam giác
a: \(\dfrac{C_{ABC}}{C_{MNP}}=\dfrac{1}{3}\)
\(\dfrac{H_{ABC}}{H_{MNP}}=\dfrac{1}{3}\)
\(\dfrac{S_{ABC}}{S_{MNP}}=k^2=\dfrac{1}{9}\)
b: Chu vi tam giác ABC là:
60:2x1=30(cm)
Chu vi tam giác MNP là:
60:2x3=90(cm)
Bài 4: Cho tam giác ABC vuông tại A, đường cao AH, biết AH = 12cm, HB= 9cm
a) Tính chu vi và diện tích tam giác ABC
b) Tính sinB, tanHAC.
Tam giác abc đường cao ah biết ab=9 bc=15 tính chu vi và diện tích tam giác abh
\(AC=\sqrt{15^2-9^2}=12\left(cm\right)\)
AH=9*12/15=7,2cm
BH=9^2/15=5,4cm
\(C_{ABH}=7.2+5.4+9=21.6\left(cm\right)\)
\(S_{ABH}=\dfrac{1}{2}\cdot5.4\cdot7.2=3.6\cdot5.4=19.44\left(cm^2\right)\)
Cho tam giác vuông ABC, \(\widehat{A}=90^0;\widehat{C}=30^0\) và đường phân giác BD (D thuộc cạnh AC)
a) Tính tỉ số \(\dfrac{AD}{CD}\)
b) Cho biết độ dài AB = 12,5cm. hãy tính chu vi và diện tích của tam giác ABC
Tính diện tích của tam giác đều ABC biết chu vi tam giác ABC bằng 18cm
A. 9 ( c m 2 ) 18 3 ( c m 2 )
B. 18 3 ( c m 2 )
C. 9 3 ( c m 2 )
D. 27 3 ( c m 2 )
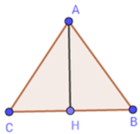
Cạnh của tam giác đều là: AB = BC = CA = 18 : 3 = 6(cm)
Gọi AH là đường cao kẻ từ đỉnh A của tam giác ABC
Khi đó AH vừa là đường cao vừa là đường trung tuyến của tam giác đều ABC.
Suy ra BH = HC = BC = 1 2 .6 = 3(cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AHB ta có:
AH = A B 2 − B H 2 = 6 2 − 3 2 = 27 = 3 3 (cm)
Diện tích tam giác đều là:
SABC = A H . B C 2 = 3 3 .6 2 = 9 3 (cm2)
Đáp án cần chọn là: C