Câu 3. Tìm tất cả các giá trị của tham số m để phương trình mcosx+m-1=0 có nghiệm thuộc đoạn 0 ; pi/2. Giúp em với, em cảm ơn.

Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số m để phương trình
4
log
4
2
x
−
2
log
2
x
+
3
−
m
0
có nghiệm thuộc đoạn
2
;
4
.
A.
2
≤
m
≤
3
. B.
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 4 log 4 2 x − 2 log 2 x + 3 − m = 0 có nghiệm thuộc đoạn 2 ; 4 .
A. 2 ≤ m ≤ 3 .
B. 2 ≤ m ≤ 4 .
C. 3 ≤ m ≤ 4 .
D. 1 ≤ m ≤ 2 .
Đáp án A
Điều kiện: x > 0 .
4 log 4 2 x − 2 log 2 x + 3 − m = 0 ⇔ 4. 1 4 . log 2 2 x − 2 log 2 x + 3 − m = 0 ⇔ log 2 2 x − 2 log 2 x + 3 − m = 0 1 .
Đặt t = log 2 x ta có (1) tương đương
t 2 − 2 t + 3 − m = 0 ⇔ t 2 − 2 t + 3 = m .
Ta tìm giá trị của m để t 2 − 2 t + 3 − m = 0 có nghiệm thuộc đoạn 1 ; 2 .
Khảo sát hàm y t = t 2 − 2 t + 3.
Ta có y ' t = 2 t − 2 = 0 ⇔ t = 1.
Bảng biến thiên
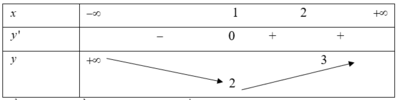
Để thỏa mãn đề bài thì 2 ≤ m ≤ 3 .
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình
4
log
2
4
x
−
2
log
2
x
+
3
−
m
0
có nghiệm thuộc đoạn
1
2
;
4
.
A.
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 4 log 2 4 x − 2 log 2 x + 3 − m = 0 có nghiệm thuộc đoạn 1 2 ; 4 .
A. 2 ; 3
B. 11 4 ; 15
C. 11 4 ; 9
D. 2 ; 6
Đáp án D
Điều kiện: x > 0.
Đặt t = log 2 x . Khi đó
4 log 2 4 x − 2 log 2 x + 3 − m = 0 ⇔ 4. 1 4 log 2 2 x − 2 log 2 x + 3 − m = 0 ⇔ t 2 − 2 t + 3 − m = 0.
Để thỏa mãn đề bài thì phương trình t 2 − 2 t + 3 − m = 0 có nghiệm thuộc đoạn − 1 ; 2
t 2 − 2 t + 3 − m = 0 ⇔ t 2 − 2 t + 3 = m .
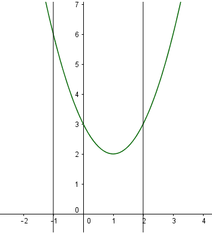
Từ đồ thị hàm số y = t 2 − 2 t + 3 nhân thấy 2 ≤ m ≤ 6 thỏa mãn điều kiện đề bài.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để phương trình:
1
3
cos
3
x
-
3
cos
2
x
+
5
cos
x
-
3
+
2
m
0
có đúng bốn nghiệm thuộc đoạn
0
;...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình: 1 3 cos 3 x - 3 cos 2 x + 5 cos x - 3 + 2 m = 0 có đúng bốn nghiệm thuộc đoạn 0 ; 2 π
A. - 3 2 < m < - 1 3
B. 1 3 ≤ m < 3 2
C. 1 3 < m < 3 2
D. - 3 2 ≤ m < - 1 3
Tìm tất cả các giá trị của m để phương trình: 2sinx + mcosx - 2m 0 có nghiệm? A.
[
m
≥
2
3
m
≤
-
2
3
B.
-
2...
Đọc tiếp
Tìm tất cả các giá trị của m để phương trình: 2sinx + mcosx - 2m = 0 có nghiệm?
A. [ m ≥ 2 3 m ≤ - 2 3
B. - 2 3 ; 2 3
C. - 2 3 ; 2 3
D. m ∈ ℝ
Đáp án C
để phương trình: 2sinx + mcosx - 2m = 0 có nghiệm
2 2 + m 2 ≥ 2 m 2 ⇔ m 2 ≤ 4 3 ⇔ - 2 3 ≤ m ≤ 2 3
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình
x
2
−
5
x
+
7
+
2
m
0
có nghiệm thuộc đoạn [1;5] A.
3
4
≤
m
≤
7
B.
−
7
2
≤
m
≤
−
3
8
C.
3
≤...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình x 2 − 5 x + 7 + 2 m = 0 có nghiệm thuộc đoạn [1;5]
A. 3 4 ≤ m ≤ 7
B. − 7 2 ≤ m ≤ − 3 8
C. 3 ≤ m ≤ 7
D. 3 8 ≤ m ≤ 7 2
Tìm tất cả các giá trị của tham số m để phương trình
1
3
cos
3
x
−
3
cos
2
x
+
5
cos
x
−
3
+
2
m
0
có đúng bốn nghiệm phân biệt thuộc đoạn
0
;...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình 1 3 cos 3 x − 3 cos 2 x + 5 cos x − 3 + 2 m = 0
có đúng bốn nghiệm phân biệt thuộc đoạn 0 ; 2 π .
A. − 3 2 < m < − 1 3
B. 1 3 ≤ m < 3 2
C. 1 3 < m < 3 2
D. − 3 2 ≤ m ≤ − 1 3
Chọn C.
Phương pháp:
Giải phương trình bằng phương pháp đặt ẩn phụ.
Cách giải:

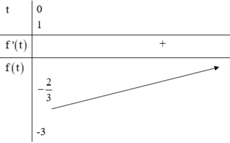
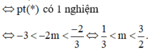
Đúng 0
Bình luận (0)
Câu 1: Tích các nghiệm trên khoảng left(dfrac{pi}{4};dfrac{7pi}{4}right)của phương trình cos2x-3cosx+20 Câu 2: Tìm tất cả các giá trị thực của tham số m để phương trình 2cos^23x+left(3-2mright)cos3x+m-20 có đúng 3 nghiệm thuộc khoảng left(-dfrac{pi}{6};dfrac{pi}{3}right).Câu 3: Tính tổng T tất cả các nghiệm của phương trình 2sin^2dfrac{x}{4}-3cosdfrac{x}{4}0 trên đoạn left[0;8piright].Câu 4: Giá trị của m để phương trình cos2x-left(2m+1right)sinx-m-10 có nghiệm trên khoảng left(0;piright) là min...
Đọc tiếp
Câu 1: Tích các nghiệm trên khoảng \(\left(\dfrac{\pi}{4};\dfrac{7\pi}{4}\right)\)của phương trình \(cos2x-3cosx+2=0\)
Câu 2: Tìm tất cả các giá trị thực của tham số m để phương trình \(2cos^23x+\left(3-2m\right)cos3x+m-2=0\) có đúng 3 nghiệm thuộc khoảng \(\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\).
Câu 3: Tính tổng T tất cả các nghiệm của phương trình \(2sin^2\dfrac{x}{4}-3cos\dfrac{x}{4}=0\) trên đoạn \(\left[0;8\pi\right]\).
Câu 4: Giá trị của m để phương trình \(cos2x-\left(2m+1\right)sinx-m-1=0\) có nghiệm trên khoảng \(\left(0;\pi\right)\) là \(m\in[a;b)\) thì a+b là?
Câu 5: Điều kiện cần và đủ để phương trình \(msinx-3cosx=5\) có nghiệm là \(m\in(-\infty;a]\cup[b;+\infty)\) với \(a,b\in Z\). Tính a+b.
Câu 6: Điều kiện để phương trình \(msinx-3cosx=5\) có nghiệm là?
Câu 7: Số nghiệm để phương trình \(sin2x+\sqrt{3}cos2x=\sqrt{3}\) trên khoảng \(\left(0;\dfrac{\pi}{2}\right)\) là?
Câu 8: Tập giá trị của hàm số \(y=\dfrac{sinx+2cosx+1}{sinx+cosx+2}\) là?
Câu 9: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn \(\left[-2018;2018\right]\) dể phương trình \(\left(m+1\right)sin^2-sin2x+cos2x=0\) có nghiệm?
Câu 10: Có bao nhiêu giá trị nguyên của tham số m để phương trình \(sin2x-cos2x+|sinx+cosx|-\sqrt{2cos^2x+m}-m=0\) có nghiệm thực?
1.
\(cos2x-3cosx+2=0\)
\(\Leftrightarrow2cos^2x-3cosx+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pm\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(x=k2\pi\in\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]\Rightarrow\) không có nghiệm x thuộc đoạn
\(x=\pm\dfrac{\pi}{3}+k2\pi\in\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]\Rightarrow x_1=\dfrac{\pi}{3};x_2=\dfrac{5\pi}{3}\)
\(\Rightarrow P=x_1.x_2=\dfrac{5\pi^2}{9}\)
Đúng 1
Bình luận (0)
2.
\(pt\Leftrightarrow\left(cos3x-m+2\right)\left(2cos3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos3x=\dfrac{1}{2}\left(1\right)\\cos3x=m-2\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x=\pm\dfrac{\pi}{9}+\dfrac{k2\pi}{3}\)
Ta có: \(x=\pm\dfrac{\pi}{9}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=\pm\dfrac{\pi}{9}\)
Yêu cầu bài toán thỏa mãn khi \(\left(2\right)\) có nghiệm duy nhất thuộc \(\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}m-2=0\\m-2=1\\m-2=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=2\\m=3\\m=1\end{matrix}\right.\)
TH1: \(m=2\)
\(\left(2\right)\Leftrightarrow cos3x=0\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=\dfrac{\pi}{6}\left(tm\right)\)
\(\Rightarrow m=2\) thỏa mãn yêu cầu bài toán
TH2: \(m=3\)
\(\left(2\right)\Leftrightarrow cos3x=0\Leftrightarrow x=\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=0\left(tm\right)\)
\(\Rightarrow m=3\) thỏa mãn yêu cầu bài toán
TH3: \(m=1\)
\(\left(2\right)\Leftrightarrow cos3x=-1\Leftrightarrow x=\dfrac{\pi}{3}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow\left[{}\begin{matrix}x=\pm\dfrac{1}{3}\\x=-1\\x=-\dfrac{5}{3}\end{matrix}\right.\)
\(\Rightarrow m=2\) không thỏa mãn yêu cầu bài toán
Vậy \(m=2;m=3\)
Đúng 2
Bình luận (0)
3.
\(2sin^2\dfrac{x}{4}-3cos\dfrac{x}{4}=0\)
\(\Leftrightarrow2cos^2\dfrac{x}{4}+3cos\dfrac{x}{4}-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos\dfrac{x}{4}=\dfrac{1}{2}\\cos\dfrac{x}{4}=-2\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow x=\pm\dfrac{4\pi}{3}+k8\pi\in\left[0;8\pi\right]\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4\pi}{3}\\x=\dfrac{20\pi}{3}\end{matrix}\right.\)
\(\Rightarrow T=\dfrac{4\pi}{3}+\dfrac{20\pi}{3}=8\pi\)
Đúng 0
Bình luận (0)
Cho phương trình
log
3
2
x
+
log
3
2
x
+
1
-
2
m
-
1
0
. Tập tất cả các giá trị của tham số m để phương trình có nghiệm thuộc đoạn
1
;
3
3
là A.
0
≤
m
≤...
Đọc tiếp
Cho phương trình log 3 2 x + log 3 2 x + 1 - 2 m - 1 = 0 . Tập tất cả các giá trị của tham số m để phương trình có nghiệm thuộc đoạn 1 ; 3 3 là
A. 0 ≤ m ≤ 1
B. 0 ≤ m ≤ 2
C. 0 ≤ m ≤ 13 6
D. 1 ≤ m ≤ 2
Điều kiện: x > 0
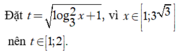
Phương trình trở thành
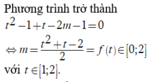
Do đó yêu cầu bài toán ![]()
Chọn B.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để phương trình msinx - mcosx = 2 vô nghiệm
\(msinx-mcosx=2\)
Phương trình có nghiệm:
\(\Leftrightarrow m^2+\left(-m\right)^2\ge2^2\)
\(\Leftrightarrow2m^2-4\ge0\Rightarrow\)\(\left[{}\begin{matrix}x\le-\sqrt{2}\\x\ge\sqrt{2}\end{matrix}\right.\)
Phương trình vô nghiệm
\(\Leftrightarrow-\sqrt{2}\le x\le\sqrt{2}\)
Đúng 1
Bình luận (0)