Điều kiện: x > 0
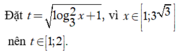
Phương trình trở thành
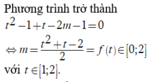
Do đó yêu cầu bài toán ![]()
Chọn B.
Điều kiện: x > 0
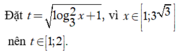
Phương trình trở thành
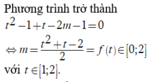
Do đó yêu cầu bài toán ![]()
Chọn B.
Cho phương trình m x 2 - 2 x + 2 + 1 - x 2 + 2 x = 0 (m là tham số). Biết rằng tập hợp tất cả các giá trị của tham số m để phương trình trên có nghiệm thuộc đoạn 1 ; 1 + 2 2 là đoạn a , b .Tính giá trị biểu thức T=2b-a.
![]()
![]()
![]()
![]()
Tập tất cả các giá trị của tham số m để phương trình 16 x - 2 ( m - 3 ) 4 x + 3 m + 1 = 0 có nghiệm là:
A. - ∞ ; - 1 3 ∪ [ 8 ; + ∞ )
B. ( - ∞ ; - 1 3 ] ∪ [ 8 ; + ∞ )
C. - ∞ ; - 1 3 ∪ ( 8 ; + ∞ )
D. ( - 1 ; 1 ] ∪ [ 8 ; + ∞ )
Cho phương trình m ln 2 x + 1 - x + 2 - m ln x + 1 - x - 2 = 0 1 . Tập tất cả giá trị của tham số m để phương trình 1 có các nghiệm, trong đó có hai nghiệm phân biệt thỏa mãn 0 < x 1 < 2 < 4 < x 2 là khoảng a ; + ∞ . Khi đó, a thuộc khoảng
A. (3,8;3,9)
B. (3,7;3,8)
C. (3,6;3,7)
D. (3,5;3,6)
Tất cả các giá trị thực của tham số m để phương trình cos 2 x - 2 m - 1 cos x - m + 1 = 0 có đúng 2 nghiệm thuộc đoạn - π 2 ; π 2 là
A. - 1 ≤ m ≤ 0
B. 0 ≤ m ≤ 1
C. - 1 ≤ m ≤ 1
D. 0 ≤ m ≤ 1
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để phương trình ( m 2 + 2 ) c o s 2 x - 2 m sin 2 x + 1 = 0 có nghiệm
A. 3
B. 7
C. 6
D. 4
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình 9 1 - x + 2 ( m - 1 ) 3 1 - x + 1 = 0 có 2 nghiệm phân biệt.
A. m > 1
B. m < -1
C. m < 0
D. -1 < m < 0
Tìm tất cả các giá trị thực của tham số m để bất phương trình ( m + 1 ) x 2 - 2 ( m + 1 ) x + 4 ≥ 0 ( 1 ) có tập nghiệm S = ℝ ?
A. m > - 1
B. - 1 ≤ m ≤ 3
C. - 1 < m ≤ 3
D. - 1 < m < 3
Cho bất phương trình m . 3 x + 1 + ( 3 m + 2 ) ( 4 - 7 ) x + ( 4 + 7 ) x > 0 với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho có nghiệm đúng với mọi x ∈ - ∞ ; 0
A. m ≥ 2 - 2 3 3
B. m > 2 - 2 3 3
C. m > 2 + 2 3 3
D. m ≥ - 2 - 2 3 3
Cho phương trình 4 x 2 - 2 x + 1 - m . 2 x 2 - 2 x + 2 + 3 m - 2 = 0 . Tập tất cả các giá trị của tham số m để phương trình đã cho có nghiệm phân biệt là
A. 2 ; + ∞
B. [ 2 ; + ∞ )
C. 1 ; + ∞
D. - ∞ ; 1 ∪ 2 ; + ∞