Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt AC tại D, trên BC lấy điểm M sao cho AB = BM. Chứng minh DM vuông góc BC
mk cần gấp , chiều nay mk thi rồi!!!
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt AC tại D, trên BC lấy điểm M sao cho AB = BM. Chứng minh DM vuông góc BC
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt AC tại D, trên BD lấy điểm M sao cho BA = BM. Chứng minh DM vuông góc BC
▲BMD và ▲BAD có
BA=BM
∠DAM=∠DBA
BD là cạnh chung
⇒▲BMD=▲BAD
⇒∠M=∠A (2 góc tương ứng)
mà ∠M=90 độ ⇒∠M=90 độ hay DM⊥BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC tại D. Trên tia BC lấy điểm M sao cho BM=BA. Chứng minh DM vuông góc với BC.
| GT | Tam giác ABC, góc A=90o, góc ABD = góc MBD, BM = BA |
| KL | DM vuông góc với BC |
- Xét \(\Delta ABD\) và \(\Delta MBD\) ta có:
BD là cạnh chung
góc ABD = góc MBD
BA = BM ( gt )
=> \(\Delta ABD=\Delta MBD\) ( Trường hợp c-g-c )
=> góc A = góc BMD ( Cặp góc tương ứng )
Góc A = 90o => góc BMD = 90o
<=> DM vuống góc với BC.
Đúng 0
Bình luận (0)
Câu 4: (2 điểm).Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC tại D, trên BC lấy điểm M sao cho AB = BM. a) Chứng minh: ABD = MBD b) Chứn minh: AD = DM; DM BC. c) Trên tia BA lấy điểm N sao cho BN = BC. Chứng minh 3 điểm N,D,M thẳng hàng.
a: Xét ΔABD và ΔMBD có
BA=BM
\(\widehat{ABD}=\widehat{MBD}\)
BD chung
Do đó: ΔABD=ΔMBD
b: Ta có: ΔABD=ΔMBD
nên DA=DM
Ta có: ΔABD=ΔMBD
nên \(\widehat{BAD}=\widehat{BMD}=90^0\)
hay DM⊥BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông góc với A , tia phân giác góc B cắt AC tại D . Trên BC lấy M sao cho BM=BA . Chứng minh DM vuông góc với BC.
Ta có hình vẽ:
Vì tia phân giác góc B cắt AC tại D nên \(ABD=DBM=\frac{ABM}{2}\)
Xét Δ ABD và Δ MBD có:
AB = BM (gt)
ABD = DBM (chứng minh trên)
BD là cạnh chung
Do đó, Δ ABD = Δ MBD (c.g.c)
=> BAD = BMD = 90o (2 góc tương ứng)
=> \(DM\perp BM\) hay \(DM\perp BC\left(đpcm\right)\)
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A (AB AC). Tia phân giác của góc ABC cắt AC tại D. Trên cạnh BC lấy M sao cho BM BA.a) Chứng minh: Tam giác ABD tam giác MBDb) Chứng minh: góc MAD góc AMD c) Trên tia đối của tia AB lấy điểm E sao cho AE AB. Lấy K thuộc tia đối của tia DA sao cho KD 2DA. BD cắt KE tại H. Chứng minh H là trung điểm của KECÁC BẠN GIÚP MIK CÂU C VỚI !!! CẢM ƠN TRƯỚC NHA
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc ABC cắt AC tại D. Trên cạnh BC lấy M sao cho BM = BA.
a) Chứng minh: Tam giác ABD = tam giác MBD
b) Chứng minh: góc MAD = góc AMD
c) Trên tia đối của tia AB lấy điểm E sao cho AE = AB. Lấy K thuộc tia đối của tia DA sao cho KD = 2DA. BD cắt KE tại H. Chứng minh H là trung điểm của KE
CÁC BẠN GIÚP MIK CÂU C VỚI !!! CẢM ƠN TRƯỚC NHA
a: Xét ΔBAD và ΔBMD có
BA=BM
góc ABD=góc MBD
BD chung
=>ΔBAD=ΔBMD
b: DA=DM
=>góc DAM=góc DMA
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác vuông ABC, góc A 90o, phân giác BD. Kẻ BD vuông góc BC tại E. Trên tia đối của tia AB lấy điểm F sao cho AF CE. Chứng minh rằng:a) BD là đường trung trực của AE.b) ADDCc) Ba điểm E, D, F thẳng hàngBài 2: Cho tam giác vuông ABC, góc A 90o , AB 6cm, AC 8cm.a) Tính BCb) Trung trực của BC cắt AC tại D và cắt AB tại F. Chứng minh góc DBC góc DCBc) Trên tia đối của tia DB lấy điểm E sao cho DEDC. Chứng minh tam giác BCE vuôngd)Chứng minh:DF là phân giác của góc ADE và BE vuôn...
Đọc tiếp
Bài 1: Cho tam giác vuông ABC, góc A = 90o, phân giác BD. Kẻ BD vuông góc BC tại E. Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chứng minh rằng:
a) BD là đường trung trực của AE.
b) AD<DC
c) Ba điểm E, D, F thẳng hàng
Bài 2: Cho tam giác vuông ABC, góc A = 90o , AB = 6cm, AC = 8cm.
a) Tính BC
b) Trung trực của BC cắt AC tại D và cắt AB tại F. Chứng minh góc DBC = góc DCB
c) Trên tia đối của tia DB lấy điểm E sao cho DE=DC. Chứng minh tam giác BCE vuông
d)Chứng minh:DF là phân giác của góc ADE và BE vuông góc CF
Bải 3: Cho tam giác đều ABC. Tia phân giác góc B cắt cạnh AC ở M. Từ A kẻ đường thẳng vuông góc với AB cắt các tia BM, BC lần lượt ở M và E. Chứng minh:
a) Tam giác ANC là tam giác cân
b) NC vuông góc BC
c) Tam giác AEC là tam giác cân
d) So sánh BC và NE
Bài 4: Cho tam giác nhọn ABC, kẻ BM vuông góc AC, CN vuông góc AB. Trên tia đối của tia BM lấy điểm D sao cho BD=AC, trên tia đối của tia CN lấy điểm E sao cho CE=AB. Chứng minh:
a) Góc ACE= góc ABD
b) Tam giác ABD = tam giác ECA
c) Tam giác AED là tam giác vuông cân
cho tam giác ABC vuông tại A tia phân giác của góc B cất AC tại D trên BC lấy M sao cho BM=BA .Chứng minh DM vuông góc với BC
Cho tam giác ABC vuông tại A. Trên tia BA lấy điểm M sao cho BM = BC. Tia phân giác của góc B cắt AC tại H. Chứng minh rằng MH vuông góc với BC.
Tham khảo:
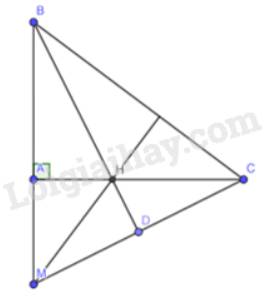
Gọi D giao điểm của tia phân giác của góc B và MC
Xét tam giác BDM và tam giác BDC có :
BD chung
\(\widehat {MBD} = \widehat {CBD}\) ( BD là phân giác của góc B)
BM = BC ( giả thiết )
( \Rightarrow \Delta BDM=\Delta BDC\)(c.g.c)
\( \Rightarrow \widehat {BDM} = \widehat {BDC}\)(2 góc tương ứng)
Mà 2 góc ở vị trí kề bù \( \Rightarrow \widehat {BDM} = \widehat {BDC} = {90^o} \Rightarrow BD \bot CM\)
Mà AC cắt BD tại H \( \Rightarrow \) H là trực tâm tam giác BMC
\( \Rightarrow \) MH là đường cao của tam giác BMC (định lí 3 đường cao đi qua trực tâm tam giác)
\( \Rightarrow \) MH vuông góc với BC
Đúng 0
Bình luận (0)