Cho hàm số y=f(x)=2x\(^2\)+1
Xác định giá trị của x nếu f(x)=9
Cho hàm số y = f(x) với tập xác định D. Trong các phát biểu sau đây phát biểu nào đúng?
A. Giá trị lớn nhất của hàm số đã cho là số lớn hơn mọi giá trị của hàm số.
B. Nếu f(x) ≤ M, ∀x ∈ D thì M là giá trị lớn nhất của hàm số y = f(x).
C. Số M = f( x 0 ) trong đó x 0 ∈ D là giá trị lớn nhất của hàm số y = f(x) nếu M > f(x), ∀x ∈ D
D. Nếu tồn tại x 0 ∈ D sao cho M = f( x 0 ) và M ≥ f(x),∀x ∈ D thì M là giá trị lớn nhất của hàm số đã cho.
Số 2 lớn hơn mọi giá trị khác của hàm số f(x) = sinx với tập xác định D = R nhưng 2 không phải là giá trị lớn nhất của hàm số này (giá trị lớn nhất là 1); vì vậy A sai. Cũng như vậy B sai với f(x) = sinx, D = R, M = 2. Phát biểu C tự mâu thuẫn: vì M = f( x 0 ), x 0 ∈ D nên hay không xảy ra M > f(x), ∀x ∈ D.
Đáp án: D
Cho hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) có \(f(0) = 1,f(1) = 2,f(2) = 5.\)
a) Hãy xác định giá trị của các hệ số \(a,b\) và \(c.\)
b) Xác định tập giá trị và khoảng biến thiên của hàm số.
Tham khảo:
a) Ta có: \(f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.\)
Lại có:
\(f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2\)
\(f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)(thỏa mãn điều kiện \(a \ne 0\))
Vậy hàm số bậc hai đó là \(y = f(x) = {x^2} + 1\)
b) Tập giá trị \(T = \{ {x^2} + 1|x \in \mathbb{R}\} \)
Vì \({x^2} + 1 \ge 1\;\forall x \in \mathbb{R}\) nên \(T = [1; + \infty )\)
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1\)
Hay \(S\left( {0;1} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:

Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
Cho hàm số y=f(x) liên tục và xác định trên R sao cho f ( x ) = x 3 + 2 x - 1 ) = x + 1 . Giá trị của tích phân ∫ 0 2 f ( 3 x + 2 ) d x tương ứng bằng
A. 12
B. 31/4
C. 15/2
D. -24/5
Cho hàm số:
Y=f(x)=-18/2x-1
A,Xác định các giá trị của x sao cho Vế phải của biểu thức có nghĩa
B,Tính f(-2);f(-1);f(1);f(2);f(3);f(-7);f(5)
C,Tính x biết y=1;y=10
D,Viết 4 cặp số xác định hàm số y=f(x)
Mong mọi người giúp đỡ càng nhanh càng tốt😶😶😶
Cho hàm số y = f(x) xác định trên tập số thực và có đạo hàm f'(x). Đồ thị hàm số y = f'(x) được cho bởi hình bên dưới. Biết rằng f(0) + f(1) - 2f(2) = f(4). - f(3). Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [0;4] là
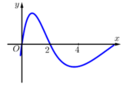
A. f(1)
B. f(0)
C. f(2)
D. f(4)
Chọn D
Từ đồ thị của hàm số y = f'(x) ta suy ra bảng biến thiên của hàm số y = f(x) trên đoạn như sau:
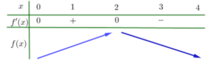
Từ bảng biến thiên, ta có nhận xét sau: ![]()
![]()
Ta lại có: f(0) + f(1) - 2f(2) = f(4). - f(3)
![]()
![]()
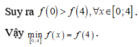
Cho hàm số y = f(x) xác định với mọi giá trị của x thuộc R.biết rằng với mọi giá trị của x ta đều có f(x)+3f(1/x)=x2 tính f(2)
Xét hàm số f(x) thỏa mãn f(x)+3f(1/x)=x^2. với mọi x thuộc R.
Đúng với x = 2 . => f(2) + 3f(1/2) = 2^2 = 4
=> f(2) + 3f(1/2) = 4 ( 1 )
Đúng với x = 1/2 => f(1/2) + 3f(2) = (1/2)^2 = 1/4.
=> 3f(2) + f (1/2) = 1/4.=> 9f(2) + 3f(1/2) = 3/4 ( 2 )
Lấy (2) trừ (1) ta đc : 8 f(2) = 3/4 - 4 = -13/4
=> f(2) = -13 / 32
Cho hàm số y = f(x) xác định trên tập số thực R và có đạo hàm f'(x) = (x - sinx)(x- m- 3)(x- \(\sqrt{9-m^2}\) )3 ∀x∈ R (m là tham số). Có bao nhiêu giá trị nguyên của m để hàm số y =f(x) đạt cực tiểu tại x = 0
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x-sinx=0\\x-m-3=0\\x-\sqrt{9-m^2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=m+3\\x=\sqrt{9-m^2}\end{matrix}\right.\)
Do hệ số bậc cao nhất của x dương nên:
- Nếu \(m=-3\Rightarrow f'\left(x\right)=0\) có nghiệm bội 3 \(x=0\) \(\Rightarrow x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m=3\Rightarrow x=0\) là nghiệm bội chẵn (không phải cực trị, ktm)
- Nếu \(m=0\Rightarrow x=3\) là nghiệm bội chẵn và \(x=0\) là nghiệm bội lẻ, đồng thời \(x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m\ne0;\pm3\) , từ ĐKXĐ của m \(\Rightarrow-3< m< 3\Rightarrow\left\{{}\begin{matrix}m+3>0\\\sqrt{9-m^2}>0\end{matrix}\right.\)
Khi đó \(f'\left(x\right)=0\) có 3 nghiệm pb trong đó \(x=0\) là nghiệm nhỏ nhất
Từ BBT ta thấy \(x=0\) là cực tiểu
Vậy \(-3\le m< 3\)
Cho hàm số y = f(x) xác định trên R\{1/2} thỏa mãn f ' ( x ) = 2 2 x - 1 ; f(0)=1 Giá trị của biểu thức f(-1)+f(3) bằng:
A. 4+ln15
B. 2+ln15
C. 3+ln15
D. ln15
Cho hàm số y = f(x) xác định và liên tục trên [-2;2], có đồ thị của hàm số y= f'(x) như sau: Tìm giá trị x 0 để hàm số y=f(x) đạt giá trị lớn nhất trên [-2;2].
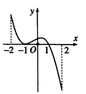
A. x 0 = 2
B. x 0 = -1
C. x 0 = -2
D. x 0 = 1
Cho hàm số được xác định bởi công thức : y = f(x) = a.x^2 = b.x + c
a, Tìm a , b , c biết f(0) = - 4 ; f(1) = - 1 ; f(-1) = - 9
b, Chứng minh rằng giá trị của hàm số ko nhận giá trị dương với mọi giá trị của biến x với a , b , c vừa tìm được ở câu a