biện luậ theo m số nghiệm của phương trình x² -2x+3=m

Những câu hỏi liên quan
Cho đồ thị hàm số y = x\(^2\) -2x - 3 :
Dựa vào đồ thị biện luận theo m số nghiệm của phương trình: x^2 - 2x - 3 + m = 0
biện luận nghiệm của hệ phương trình sau theo m:
\(\left\{{}\begin{matrix}\sqrt{2x}+\sqrt{3-y}=m\\\sqrt{2y}+\sqrt{3-x}=m\end{matrix}\right.\)
biện luận theo m số nghiệm của phương trình x² -2x=3=m
=>x^2-2x+3-m=0
Δ=(-2)^2-4(3-m)
=4-12+4m=4m-8
Để phương trình vô nghiệm thì 4m-8<0
=>m<2
Để phương trình có nghiệm kép thì 4m-8=0
=>m=2
Để phương trình có hai nghiệm phân biệt thì 4m-8>0
=>m>2
Đúng 0
Bình luận (0)
Biện luận số nghiệm theo m của phương trình:
x^2-|x|+m=0
+ Biện luận theo tham số m số nghiệm của phương trình x^2 - 4|x| + m = 0.
Biện luận theo tham số m số nghiệm của phương trình: x 4 - 6 x 2 + 3 = m .
Ta có: x 4 - 6 x 2 + 3 = m
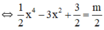
Số nghiệm của phương trình (*) chính bằng số giao điểm của đồ thị (C) và đường thẳng (d) y = m/2.
Từ đồ thị (C) nhận thấy :
+ m/2 < - 3 ⇔ m < -6
⇒ đường thẳng (d) không cắt đồ thị (C)
⇒ Phương trình vô nghiệm.
+ m/2 = -3 ⇔ m = -6
⇒ đường thẳng (d) cắt đồ thị (C) tại hai điểm cực tiểu
⇒ Phương trình có 2 nghiệm.
+ -3 < m/2 < 3/2 ⇔ -6 < m < 3
⇒ đường thẳng (d) cắt (C) tại 4 điểm phân biệt
⇒ Phương trình có 4 nghiệm.
+ m/2 = 3/2 ⇔ m = 3
⇒ đường thẳng (d) cắt (C) tại ba điểm
⇒ phương trình có 3 nghiệm.
+ m/2 > 3/2 ⇔ m > 3
⇒ đường thẳng (d) cắt (C) tại hai điểm
⇒ phương trình có hai nghiệm phân biệt.
Vậy:
+) m < - 6 thì phương trình vô nghiệm.
+) m = - 6 hoặc m > 3 thì PT có 2 nghiệm.
+) m = 3 thì PT có 3 nghiệm.
+) – 6 < m < 3 thì PT có 4 nghiệm.
Đúng 0
Bình luận (0)
Cho hàm số y=\(\frac{2x-3}{x-2}\) (C),
a) Khảo sát và vẽ đồ thị hàm số (C).
b) Biện luận theo m số nghiệm của phương trình \(\frac{2x-3}{\left|x-2\right|}\)=m
Cho phương trình : m2x+3=9x+m (1)
a, Giải phương trình khi m=3
b, Tìm m để phương trình nhận x=1/6 làm nghiệm
c, Giải và biện luận số nghiệm của phương trình (1) theo tham số m.
d, Khi m>3, tìm min: A= 16x+4m+14
nhờ các bạn giải giúp mk câu d là được
.cho phương trình ẩn x:ax2+(b-m)x+c=0 .Viết chương trình :
a) giải phương trình với hệ số a=0.
b)biện luận nghiệm của phương trình theo tham số m.
















