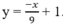Ta có: x 4 - 6 x 2 + 3 = m
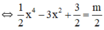
Số nghiệm của phương trình (*) chính bằng số giao điểm của đồ thị (C) và đường thẳng (d) y = m/2.
Từ đồ thị (C) nhận thấy :
+ m/2 < - 3 ⇔ m < -6
⇒ đường thẳng (d) không cắt đồ thị (C)
⇒ Phương trình vô nghiệm.
+ m/2 = -3 ⇔ m = -6
⇒ đường thẳng (d) cắt đồ thị (C) tại hai điểm cực tiểu
⇒ Phương trình có 2 nghiệm.
+ -3 < m/2 < 3/2 ⇔ -6 < m < 3
⇒ đường thẳng (d) cắt (C) tại 4 điểm phân biệt
⇒ Phương trình có 4 nghiệm.
+ m/2 = 3/2 ⇔ m = 3
⇒ đường thẳng (d) cắt (C) tại ba điểm
⇒ phương trình có 3 nghiệm.
+ m/2 > 3/2 ⇔ m > 3
⇒ đường thẳng (d) cắt (C) tại hai điểm
⇒ phương trình có hai nghiệm phân biệt.
Vậy:
+) m < - 6 thì phương trình vô nghiệm.
+) m = - 6 hoặc m > 3 thì PT có 2 nghiệm.
+) m = 3 thì PT có 3 nghiệm.
+) – 6 < m < 3 thì PT có 4 nghiệm.