Tìm GTLN và GTNN của các hàm số sau trên một đoạn cho trước:
y = sinx trên đoạn [\(\dfrac{-\Pi}{4}\);\(\dfrac{3\Pi}{4}\)]
Những câu hỏi liên quan
Tìm GTLN, GTNN của hàm số:
a, \(y=Cosx\) trên đoạn \([-\dfrac{\pi}{2};\dfrac{\pi}{2}]\)
b, \(y=Sinx\) trên đoạn \([-\dfrac{\pi}{2};0]\)
a, Đồ thị hàm số \(y=cosx\): \(\left(A=\left(-\dfrac{\pi}{2};0\right);B=\left(\dfrac{\pi}{2};0\right)\right)\)
Dựa vào đồ thị ta có \(\left\{{}\begin{matrix}y_{min}=0\\y_{max}=1\end{matrix}\right.\)
b, Đồ thị hàm số \(y=sinx\): \(\left(A=\left(-\dfrac{\pi}{2};-1\right);A=\left(\dfrac{\pi}{2};1\right)\right)\)
Đúng 1
Bình luận (2)
Tìm GTLN; GTNN của các hàm số:
\(a,y=2sin^2x-cos2x\)
\(b,y=3\sqrt{1+sinx}-1\) trên đoạn \(\left[0;\dfrac{\pi}{3}\right]\)
a, \(y=2sin^2x-cos2x=1-2cos2x\)
Vì \(cos2x\in\left[-1;1\right]\Rightarrow y=2sin^2x-cos2x\in\left[-1;3\right]\)
\(\Rightarrow\left\{{}\begin{matrix}y_{min}=-1\\y_{max}=3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm GTNN, GTLN của hàm số y= 2sin2x + 3cosx -1 trên đoạn \(\left[\dfrac{-\pi}{3};\dfrac{2\pi}{3}\right]\)
Tìm GTLN; GTNN của các hàm số
\(a,y=3-4sin^2xcos^2x\)
\(b,y=\dfrac{-2}{3sinx-5}\) trên đoạn \(\left[0;\dfrac{\pi}{2}\right]\)
a, \(y=3-4sin^2x.cos^2x=3-sin^22x\)
Đặt \(sin2x=t\left(t\in\left[-1;1\right]\right)\).
\(\Rightarrow y=f\left(t\right)=3-t^2\)
\(\Rightarrow y_{min}=minf\left(t\right)=2\)
\(y_{max}=maxf\left(t\right)=3\)
Đúng 1
Bình luận (0)
b, \(y=f\left(t\right)=\dfrac{-2}{3t-5}\left(t\in\left[0;1\right]\right)\)
\(\Rightarrow y_{min}=minf\left(t\right)=\dfrac{2}{5}\)
\(y_{max}=maxf\left(t\right)=1\)
Đúng 1
Bình luận (0)
Tìm GTLN, GTNN của hàm số y = sinx + cosx trên đoạn [ π/4 ; π/2 ]
16 tháng 9 2021 lúc 22:06
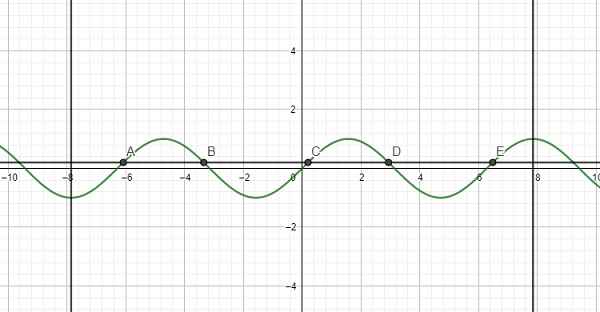
Dựa vào đồ thị của hàm số y=sinx hãy tìm số nghiệm của phương trình: sinx=1/2018 trên đoạn \(\left[-\dfrac{5\pi}{2};\dfrac{5\pi}{2}\right]\)
\(0< \dfrac{1}{2018}< 1\)
Kẻ 1 đường thẳng nằm ngang nằm giữa \(y=0\) và \(y=1\) ta thấy cắt đồ thị tại 5 điểm trên đoạn đã cho
\(\Rightarrow\) Pt có 5 nghiệm
Đúng 1
Bình luận (0)
Tìm GTNN và GTLN của hàm số sau:
1.\(y=cosx+cos\left(x-\dfrac{\pi}{3}\right)\)
2.\(y=sin^4x+cos^4x\)
3.\(y=3-2\left|sinx\right|\)
2.
$y=\sin ^4x+\cos ^4x=(\sin ^2x+\cos ^2x)^2-2\sin ^2x\cos ^2x$
$=1-\frac{1}{2}(2\sin x\cos x)^2=1-\frac{1}{2}\sin ^22x$
Vì: $0\leq \sin ^22x\leq 1$
$\Rightarrow 1\geq 1-\frac{1}{2}\sin ^22x\geq \frac{1}{2}$
Vậy $y_{\max}=1; y_{\min}=\frac{1}{2}$
Đúng 0
Bình luận (0)
3.
$0\leq |\sin x|\leq 1$
$\Rightarrow 3\geq 3-2|\sin x|\geq 1$
Vậy $y_{\min}=1; y_{\max}=3$
Đúng 0
Bình luận (0)
1.
\(y=\cos x+\cos (x-\frac{\pi}{3})=\cos x+\frac{1}{2}\cos x+\frac{\sqrt{3}}{2}\sin x\)
\(=\frac{3}{2}\cos x+\frac{\sqrt{3}}{2}\sin x\)
\(y^2=(\frac{3}{2}\cos x+\frac{\sqrt{3}}{2}\sin x)^2\leq (\cos ^2x+\sin ^2x)(\frac{9}{4}+\frac{3}{4})\)
\(\Leftrightarrow y^2\leq 3\Rightarrow -\sqrt{3}\leq y\leq \sqrt{3}\)
Vậy $y_{\min}=-\sqrt{3}; y_{max}=\sqrt{3}$
Đúng 0
Bình luận (0)
Tìm GTLN và GTNN của hàm số:
y=\(\sqrt{5-2sin^2xcos^2x}\)
y= sinx trên \(\left[\frac{\pi}{6};\frac{3\pi}{4}\right]\)
Tìm GTLN và GTNN của hàm số
y
x
5
-
5
x
4
+
5
x
3
+
1
trên đoạn [-1;2] A.
m
i
n
x
∈
[
-
1
;
2
]
y
-
10...
Đọc tiếp
Tìm GTLN và GTNN của hàm số y = x 5 - 5 x 4 + 5 x 3 + 1 trên đoạn [-1;2]
A. m i n x ∈ [ - 1 ; 2 ] y = - 10 , m a x x ∈ [ - 1 ; 2 ] y = 2
B. m i n x ∈ [ - 1 ; 2 ] y = - 2 , m a x x ∈ [ - 1 ; 2 ] y = 10
C. m i n x ∈ [ - 1 ; 2 ] y = - 10 , m a x x ∈ [ - 1 ; 2 ] y = - 2
D. m i n x ∈ [ - 1 ; 2 ] y = - 7 , m a x x ∈ [ - 1 ; 2 ] y = 1
Đáp án A
Ta có: y’ = y ’ = 5 x 4 - 20 x 3 + 15 x 2
Ta có bảng biến thiên :
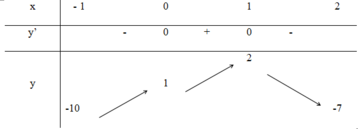
=> y’ = 0 ⇔ x = 0 (tm) hoặc x = 1(tm) hoặc x = 3 (không tm)
Vậy giá trị lớn nhất, nhỏ nhất của hàm trên [-1;2] lần lượt là 2 và -10
Đúng 0
Bình luận (0)