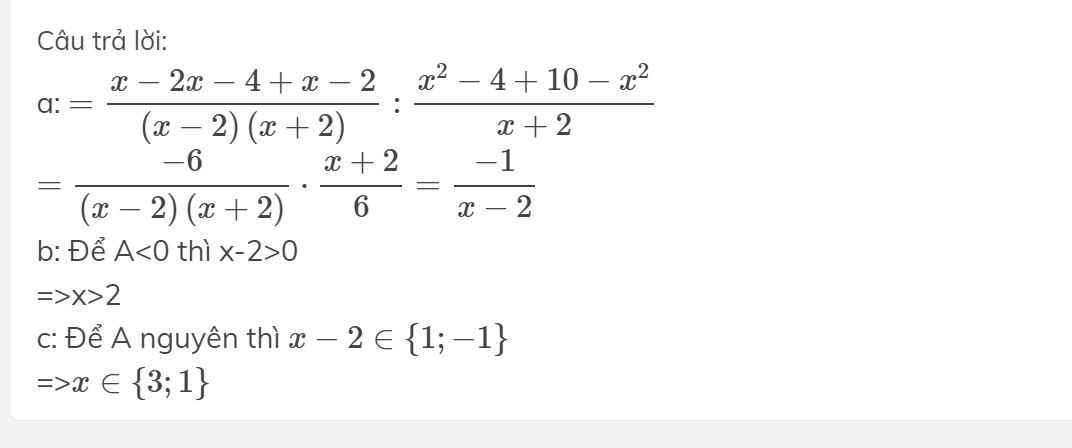hình như đề hơi sai sai á bạn

bạn ktra lại thử xem

\(P=\frac{2\left(x-2\right)\left(x+2\right)}{x^2+x+5}.\frac{5\left(x^2+x+5\right)}{\left(x-4\right)\left(x+3\right)}.\frac{\left(x-1\right)\left(x-4\right)}{10\left(x-2\right)\left(x+2\right)}=\frac{x-1}{x+3}\)

ĐK: \(x\ne\left\{4;-3;1;2;-2\right\}\)

b, \(P\in Z\Rightarrow\frac{x-1}{x+3}\in Z\Rightarrow x-1⋮\left(x+3\right)\Rightarrow-4⋮\left(x+3\right)\Rightarrow\left(x+3\right)\in\left\{-4;-2;-1;1;2;4\right\}\)

\(\Rightarrow x\in\left\{-7;-5;-4;-2;-1;1\right\}\)

\(\Rightarrow P\in\left\{2;3;5;-3;-1;0\right\}\)

\(a,A=\dfrac{x\left(x+2\right)+\left(2-x\right)\left(x-2\right)+12-10x}{\left(x-2\right)\left(x+2\right)}\)

\(=\dfrac{x^2+2x+2x-4-x^2+2x+12-10x}{\left(x-2\right)\left(x+2\right)}\)

\(=\dfrac{-4x+8}{\left(x-2\right)\left(x+2\right)}\)

\(=\dfrac{-4\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)

\(=-\dfrac{4}{x+2}\)

Vậy \(A=-\dfrac{4}{\left(x+2\right)}\)

a: Thay x=5 vào B, ta được:

\(B=\dfrac{5-1}{5-3}=\dfrac{4}{2}=2\)

b:  \(A=\dfrac{2x^2+6x-2x^2-3x-1}{\left(x-3\right)\left(x+3\right)}=\dfrac{3x-1}{\left(x+3\right)\left(x-3\right)}\)

a: \(A=\left(\dfrac{2x^2+2}{x^3-1}+\dfrac{x^2-x+1}{x^4+x^2+1}-\dfrac{x^2+3}{x^3-x^2+3x-3}\right):\dfrac{1}{x-1}\)

\(=\left(\dfrac{2x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{x^2-x+1}{x^4+2x^2+1-x^2}-\dfrac{x^2+3}{x^2\left(x-1\right)+3\left(x-1\right)}\right)\cdot\dfrac{x-1}{1}\)

\(=\left(\dfrac{2x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{\left(x^2-x+1\right)}{\left(x^2+1\right)^2-x^2}-\dfrac{x^2+3}{\left(x-1\right)\left(x^2+3\right)}\right)\cdot\dfrac{x-1}{1}\)

\(=\left(\dfrac{2x^2+3}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{x^2-x+1}{\left(x^2+1+x\right)\left(x^2+1-x\right)}-\dfrac{1}{x-1}\right)\cdot\dfrac{x-1}{1}\)

\(=\left(\dfrac{2x^2+3}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{1}{x^2+x+1}-\dfrac{1}{x-1}\right)\cdot\dfrac{x-1}{1}\)

\(=\dfrac{2x^2+3+x-1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{x-1}{1}\)

\(=\dfrac{x^2+1}{x^2+x+1}\)

b: Để A là số nguyên thì \(x^2+1⋮x^2+x+1\)

=>\(x^2+x+1-x⋮x^2+x+1\)

=>\(x⋮x^2+x+1\)

=>\(x^2+x⋮x^2+x+1\)

=>\(x^2+x+1-1⋮x^2+x+1\)

=>\(-1⋮x^2+x+1\)

=>\(x^2+x+1\in\left\{1;-1\right\}\)

=>\(x^2+x+1=1\)

=>x²+x=0

=>x(x+1)=0

=>\(x\in\left\{0;-1\right\}\)

a: \(Q=\left(\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}-2}{x-1}\right)\cdot\left(x+\sqrt{x}\right)\)

\(=\left(\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right)\cdot\left(x+\sqrt{x}\right)\)

\(=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2\cdot\left(\sqrt{x}-1\right)}\cdot\sqrt{x}\cdot\left(\sqrt{x}+1\right)\)

\(=\dfrac{x+\sqrt{x}-2-\left(x-\sqrt{x}-2\right)}{\left(\sqrt{x}+1\right)\cdot\left(\sqrt{x}-1\right)}\cdot\sqrt{x}\)

\(=\dfrac{x+\sqrt{x}-2-x+\sqrt{x}+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\sqrt{x}\)

\(=\dfrac{2\sqrt{x}\cdot\sqrt{x}}{x-1}=\dfrac{2x}{x-1}\)

b: Để Q là số nguyên thì \(2x⋮x-1\)

=>\(2x-2+2⋮x-1\)

=>\(2⋮x-1\)

=>\(x-1\in\left\{1;-1;2;-2\right\}\)

=>\(x\in\left\{2;0;3;-1\right\}\)

Kết hợp ĐKXĐ, ta được: \(x\in\left\{0;2;3\right\}\)

\(A=\left(\dfrac{x}{x^2-4}+\dfrac{2}{2-x}+\dfrac{1}{x+2}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\)

\(\Rightarrow A=\left(\dfrac{x-2\left(x+2\right)+1\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\right):\left(\dfrac{\left(x-2\right)\left(x+2\right)+10-x^2}{x+2}\right)\)

\(\Rightarrow A=\left(\dfrac{-6}{x^2-4}\right):\left(\dfrac{6}{x+2}\right)\)

\(\Rightarrow A=-\dfrac{6}{x^2-4}.\dfrac{x+2}{6}=-\dfrac{6\left(x+2\right)}{\left(x-2\right)\left(x+2\right)6}=-\dfrac{1}{x-2}\)

để A<0 thì :

\(\left\{{}\begin{matrix}x-2\ne0\\x-2\notin Z-\end{matrix}\right.\)\(\Leftrightarrow x\in\left\{3;4;5;6;7;8;9;....n\right\}\)

( Z- là tập hợp số nguyên âm )

Để A có giá trị nguyên thì :

\(\left\{{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)

\(Q=\frac{\sqrt{x}\cdot\left(\sqrt{x}-1\right)\cdot\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}-\frac{\sqrt{x}\cdot\left(2\sqrt{x}+1\right)}{\sqrt{x}}+\frac{2\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}-1\right)}{\sqrt{x}-1}\)

\(Q=x-\sqrt{x}-2\sqrt{x}-1+2\sqrt{x}+2\)

\(Q=x+1\)

Không thể tìm được GTLN hay GTNN của Q.

b)

   \(\frac{3x+3}{\sqrt{x}}=3\sqrt{x}+\frac{3}{\sqrt{x}}\)

Để \(\frac{3Q}{\sqrt{x}}\) nguyên thì \(\frac{3}{\sqrt{x}}\)nguyên hay \(\sqrt{x}\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)

Vì \(\sqrt{x}\)dương nên \(\sqrt{x}\in\left\{1;3\right\}\)

Vậy x=1, x=9 là các giá trị cần tìm