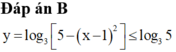Tìm max P= ( - x2-2x+2016)/x2

Những câu hỏi liên quan
tìm min, max của các biểu thức sau
a, √ x2-2x+5
b, 2 + √x2-4x+5
Không có max
`a)sqrt{x^2-2x+5}`
`=sqrt{x^2-2x+1+4}`
`=sqrt{(x-1)^2+4}`
Vì `(x-1)^2>=0`
`=>(x-1)^2+4>=4`
`=>sqrt{(x-1)^2+4}>=sqrt4=2`
Dấu "=" xảy ra khi `x=1.`
`b)2+sqrt{x^2-4x+5}`
`=2+sqrt{x^2-4x+4+1}`
`=2+sqrt{(x-2)^2+1}`
Vì `(x-2)^2>=0`
`=>(x-2)^2+1>=1`
`=>sqrt{(x-2)^2+1}>=1`
`=>sqrt{(x-2)^2+1}+2>=3`
Dấu "=" xảy ra khi `x=2`
Đúng 3
Bình luận (2)
Tìm Max (GTLN) của Q=-x2-2x+2021
Ta có: \(Q=-x^2-2x+2021\)
\(=-\left(x^2+2x+1-2022\right)\)
\(=-\left(x+1\right)^2+2022\le2022\forall x\)
Dấu '=' xảy ra khi x=-1
Đúng 2
Bình luận (0)
\(Q=-\left(x^2+2x+1\right)+2022\)
\(Q=-\left(x+1\right)^2+2022\le2022\)
\(Q_{max}=2022\) khi \(x=-1\)
Đúng 2
Bình luận (0)
Tìm GTLN (max) của hàm số
y
log
3
4
+
2
x
-
x
2
A.
log
3
4
B.
log
3
5
C.
5
3
D. ...
Đọc tiếp
Tìm GTLN (max) của hàm số y = log 3 4 + 2 x - x 2
A. log 3 4
B. log 3 5
C. 5 3
D. 1 + 3
Cho \(x^2-2x-m^2+4m-3=0\) 0
Tìm m/ phương trình có 2 nghiệm âm . Gọi x1, x2 là 2 nghiệm phương trình . Tìm m/ (x1 + x2 )x2 max
Tìm GTLN (max), GTNN (min) của
y
x
2
-
x
+
2
x
-
1
khi
x
∈
3
2
;
3
Đọc tiếp
Tìm GTLN (max), GTNN (min) của y = x 2 - x + 2 x - 1 khi x ∈ 3 2 ; 3
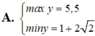
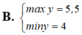
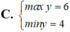
Tìm min của biểu thức(áp dụngBđtCauchy)
Q= (x2 + 2x+1)/(x+2)
R= (x2 -x+4)+ 1/( x 2 -x -1)
S=(x2 +x+1)/ (x2 +2x+1)
TÌM MAX CỦA BIỂU THỨc
A= x/(x+2004)2 với x>0
B= 3/(4x2 - 4x+5)
C= (x2 -6x+14)/ (x2- 6x+12)
Giúp mk với, đúng mình tick cho , mình cần gấp lắm, làm câu nào cũng được nhé!! Được hết ccàng tốt)
Tìm Min = x^2 - 2x + 2016
Tìm Max = -x^2 +2x + 2016
x^2-2x+2016=(x-1)^2+2015>=2015
=> min của x^2-2x+2016=2015 khi x =1
-x^2+2x+2016=-(x-1)^2+2017=<2017
=> max -x^2+2x+2016 =2017 khi x=1
Đúng 0
Bình luận (0)
Cho x2−2(m−1)x+(m+1)2=0x2−2(m−1)x+(m+1)2=0 có 2 nghiệm x1, x2 t/m x1+x2≤4x1+x2≤4. Tìm MAX, MIN của P=x31+x32+x1.x2(3x1+3x2)+8x1.x2
Cho x2+y2+xy=3.Tìm Min và Max M=x2+y2-xy
giúp với mấy b.n!\
\(\dfrac{M}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{3\left(x^2+y^2+xy\right)-2\left(x^2+y^2+2xy\right)}{x^2+y^2+xy}=3-\dfrac{2\left(x+y\right)^2}{x^2+y^2+xy}\le3\)
\(\Rightarrow M\le9\)
\(M_{max}=9\) khi \(\left\{{}\begin{matrix}x+y=0\\x^2+y^2+xy=3\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(-\sqrt{3};\sqrt{3}\right);\left(\sqrt{3};-\sqrt{3}\right)\)
\(\dfrac{M}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{\dfrac{1}{3}\left(x^2+y^2+xy\right)+\dfrac{2}{3}\left(x^2+y^2-2xy\right)}{x^2+y^2+xy}=\dfrac{1}{3}+\dfrac{2\left(x-y\right)^2}{3\left(x^2+y^2+xy\right)}\ge\dfrac{1}{3}\)
\(\Rightarrow M\ge1\)
\(M_{min}=1\) khi \(\left\{{}\begin{matrix}x-y=0\\x^2+y^2+xy=3\end{matrix}\right.\) \(\Rightarrow x=y=\pm1\)
Đúng 4
Bình luận (0)
cho x;yϵR thỏa mãn x2+y2-xy=4 tìm max và min của C=x2+y2
\(\dfrac{x^2+y^2}{2}\ge xy\Rightarrow-xy\ge-\dfrac{x^2+y^2}{2}\)
\(\Rightarrow4=x^2+y^2-xy\ge x^2+y^2-\dfrac{x^2+y^2}{2}=\dfrac{x^2+y^2}{2}\)
\(\Rightarrow x^2+y^2\le8\)
\(C_{max}=8\) khi \(x=y=\pm2\)
\(x^2+y^2\ge-2xy\Rightarrow-xy\le\dfrac{x^2+y^2}{2}\)
\(4=x^2+y^2-xy\le x^2+y^2+\dfrac{x^2+y^2}{2}=\dfrac{3}{2}\left(x^2+y^2\right)\)
\(\Rightarrow x^2+y^2\ge\dfrac{8}{3}\)
\(C_{min}=\dfrac{8}{3}\) khi \(\left(x;y\right)=\left(-\dfrac{2}{\sqrt{3}};\dfrac{2}{\sqrt{3}}\right);\left(\dfrac{2}{\sqrt{3}};-\dfrac{2}{\sqrt{3}}\right)\)
Đúng 1
Bình luận (1)
 Đúng thì like giúp mik nha bạn. Thx bạn
Đúng thì like giúp mik nha bạn. Thx bạn
Đúng 1
Bình luận (0)