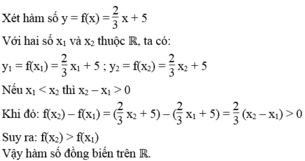Chứng minh hàm số f(x) = x\(^3\) +3x - 1 đồng biến trên R

Những câu hỏi liên quan
cho hàm số y=f(x)=3x-2, chứng minh hàm số luôn đồng biến trên R
\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{3x_1-2-3x_2+2}{x_1-x_2}=3\)
Vậy: Hàm số đồng biến trên R
Đúng 1
Bình luận (0)
Hàm số \(y=f\left(x\right)=3x-2\) có \(a=3>0\) nên hàm số luôn đồng biến trên R.
Đúng 1
Bình luận (0)
Cho hàm số bậc nhất y f(x) 3x + 1.Cho x hai giá trị bất kì
x
1
,
x
2
, sao cho
x
1
x
2
. Hãy chứng minh
f
(
x
1
)
f
(
x
2
)
rồi rút ra kết...
Đọc tiếp
Cho hàm số bậc nhất y = f(x) = 3x + 1.
Cho x hai giá trị bất kì x 1 , x 2 , sao cho x 1 < x 2 . Hãy chứng minh f ( x 1 ) < f ( x 2 ) rồi rút ra kết luận hàm số đồng biến trên R.
Do x 1 < x 2 nên x 1 − x 2 < 0
Ta có:
f x 1 − f x 2 = 3 x 1 + 1 − 3 x 2 + 1 = 3 x 1 − x 2 < 0 ⇔ f x 1 < f x 2
Vậy hàm số y = 3x + 1 đồng biến trên R
Đúng 0
Bình luận (0)
Cho hàm số bậc nhất y = f(x) = 3x + 1.
Cho x hai giá trị bất kì x1, x2, sao cho x1 < x2. Hãy chứng minh f(x1) < f(x2) rồi rút ra kết luận hàm số đồng biến trên R.
Do x1 < x2 nên x1 - x2 < 0
Ta có: f(x1 ) - f(x2 )=(3x1 + 1) - (3x2 + 1) = 3(x1 - x2 ) < 0
⇔ f(x1 ) < f(x2 )
Vậy hàm số y = 3x + 1 đồng biến trên R
Đúng 0
Bình luận (0)
hàm số y= f(x) = x^3 + 3x +1 đồng biến hay nghịch biến trên R
Cho hàm số y f(x) 3x.Cho x hai giá trị bất kì
x
1
,
x
2
sao cho
x
1
x
2
Hãy chứng minh
f
(
x
1
)
f
(
x
2
)
rồi rút ra kết luận hàm số đã cho đồng biến trên R.
Đọc tiếp
Cho hàm số y = f(x) = 3x.
Cho x hai giá trị bất kì x 1 , x 2 sao cho x 1 < x 2
Hãy chứng minh f ( x 1 ) < f ( x 2 ) rồi rút ra kết luận hàm số đã cho đồng biến trên R.
Cho x các giá trị bất kì x 1 , x 2 sao cho x 1 < x 2
= > x 1 - x 2 < 0
Ta có:
f x 1 = 3 x 1 ; f x 2 = 3 x 2 ⇒ f x 1 − f x 2 = 3 x 1 − 3 x 2 = 3 x 1 − x 2 < 0 ⇒ f x 1 < f x 2
Vậy với x 1 < x 2 ta được f ( x 1 ) < f ( x 2 ) nên hàm số y = 3x đồng biến trên tập hợp số thực R.
Đúng 0
Bình luận (0)
Cho hàm số y = f(x) = 3x.
Cho x hai giá trị bất kì x1, x2 sao cho x1 < x2.
Hãy chứng minh f(x1) < f(x2) rồi rút ra kết luận hàm số đã cho đồng biến trên R.
Cho x các giá trị bất kì x1, x2 sao cho x1 < x2
=> x1 - x2 < 0
Ta có: f(x1) = 3x1 ; f( x2) = 3x2
=> f(x1) - f(x2) = 3x1 - 3x2 = 3(x1 - x2) < 0
=> f(x1) < f(x2)
Vậy với x1 < x2 ta được f(x1) < f(x2) nên hàm số y = 3x đồng biến trên tập hợp số thực R.
Đúng 0
Bình luận (0)
Cho hàm số y = f(x) = 2 3 x + 5 với x ∈ R. Chứng minh rằng hàm số đồng biến trên R.
Cho f(x)=5x-1. Chứng minh hàm số đồng biến trên R.
Cho hàm số bậc nhất y=f(x)=(m^2+m+1)x+5.Chứng minh rằng:hàm số luôn đồng biến trên R
`a=m^2+m+1=m^2+2.m. 1/2 + (1/2)^2 + 3/4= (m+1/2)^2 + 3/4 >0 forall m`
`=> a>0 =>` Hàm số luôn đồng biến trên `RR`.
Đúng 2
Bình luận (2)
Để hàm số trên đồng biến khi \(m^2+m+1=m^2+m+\dfrac{1}{4}+\dfrac{3}{4}=\left(m+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
Vậy hàm số luôn đồng biến trên R
Đúng 2
Bình luận (1)
Ta có: \(m^2+m+1\)
\(=m^2+2\cdot m\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(m+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall m\)
Do đó: Hàm số \(f\left(x\right)=\left(m^2+m+1\right)x+5\) luôn đồng biến trên R
Đúng 1
Bình luận (1)
Cho hàm số y = f(x) = 3x.
Cho x hai giá trị bất kì x1, x2 sao cho x1 < x2 .
Hãy chứng minh f(x1 ) < f(x2 ) rồi rút ra kết luận hàm số đã cho đồng biến trên R.
Cho hàm số: y = f(x) = 3x. Cho x hai giá trị bất kì x1, x2 sao cho x1 < x2. Chứng minh f(x1) < f(x2) rồi rút ra kết luận hàm số đã cho đồng biến trên
------------
thay x1 vào f(x) ta được f(x1)=3x1
thay x2 và f(x) ta được f(x2)=3x2
lấy f(x1)-f(x2)=3x1-3x2=3(x1-x2)(1)
ta có x1<x2=>x1-x2<0
=> (1) <0
<=>f(x1)-f(x2)<0
<=>f(x1)<f(x2)
=> hàm số đã cho đồng biến
bài làm của Nguyễn Thị Thu Trang
Đúng 0
Bình luận (0)
Từ x1 < x2 và 3 > 0 suy ra 3x1< 3x2 hay f(x1) < f(x2 ).
Vậy hàm số đã cho đồng biến trên R.
P/s: Làm theo cách ngắn gọn nhé Songoku Sky Fc11.
Đúng 0
Bình luận (0)