6x^2+11x-10x
2x^2-3x-14
x^3-9x^2+6x+16
Những câu hỏi liên quan
Phân tích đa thức thành nhân tử
a)x3-9x2+6x+16
b)x3-6x2-x+30
c)3x2+22xy+11x+37y+7y2+10
Phân tích đa thức thành nhân tử
a) x^3+5x^2+3x-9
b)x^3+6x^2+11x+6
c)x^3+5x^2-3x-15
d)3x^3-4x^2+12x-16
e)2x^4-9x^2-5
Quy đồng phân thức sau: a:11x-3/3x^2-15x-42,8/x^2-6x-7,13x/9x-63. b:2/x^2+2x,3x^2-6x/x^2-2x+4,10x^2+28-8/x^4+8x mình cần gấp ạ
Quy đồng phân thức sau: a:11x-3/3x^2-15x-42,8/x^2-6x-7,13x/9x-63. b:2/x^2+2x,3x^2-6x/x^2-2x+4,10x^2+28-8/x^4+8x mình cần gấp ạ
a) Tìm MTC:
\(\text{2x + 6 = 2(x + 3)}\)
\(\text{x2 – 9 = (x – 3)(x + 3)}\)
\(\text{MTC = 2(x – 3)(x + 3) = 2(x2 – 9)}\)
Nhân tử phụ:
\(\text{2(x – 3)(x + 3) : 2(x + 3) = x – 3}\)
\(\text{2(x – 3)(x + 3) : (x2 – 9) = 2}\)
Qui đồng:
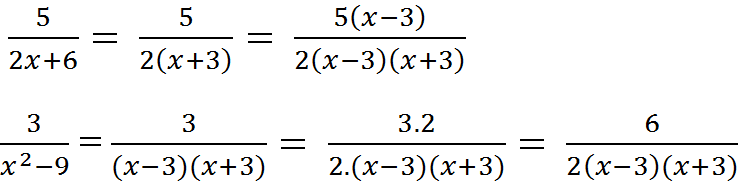
b) Tìm MTC:
Đúng 0
Bình luận (0)
Sử dụng phương pháp hệ số bất định để phân tích đa thức thành nhân tử
1, B=\(3x^3-14x^2+14x+3\)
2, C=\(x^4-6x^3+11x^2-6x+1\)
1:\(=3x^3-9x^2-5x^2+15x-x+3\)
\(=\left(x-3\right)\left(3x^2-5x-1\right)\)
2: \(=x^4-3x^3+x^2-3x^3+9x^2-3x+x^2-3x+1\)
\(=\left(x^2-3x+1\right)^2\)
Đúng 0
Bình luận (0)
Thực hiện phép chia:
a) \((3x^5-9x^6+12x^9):3x\)
b) \((6x^4+4x^3+8x^2):(2x)\)
c) \((8x^6+16x^5-10x^4):(2x^4)\)
d) \((4x^4+6x^5+14x^7):(2x^3)\)
a: =x^4-3x^5+4x^8
b: =2x^3+2x^2+4x
c: =4x^2+8x-5
d: =2x+3x^2+7x^4
Đúng 1
Bình luận (0)
BÀI 1 : RÚT GỌN CÁC BIỂU THỨC SAU .
a, \(\dfrac{3}{x-3}-\dfrac{6x}{9-x^2}+\dfrac{x}{x+3}\)
b, \(\left(\dfrac{3x}{1-3x}+\dfrac{2x}{3x+1}\right):\dfrac{6x^2+10x}{9x^2-6x+1}\)
c, \(\left(\dfrac{9}{x^3-9x}+\dfrac{1}{x+3}\right):\left(\dfrac{x-3}{x^2+3x}-\dfrac{x}{3x+9}\right)\)
d, \(\dfrac{1-x^2}{x}\left(\dfrac{x^2}{x+3}-1\right)+\dfrac{3x^2-14x+3}{x^2+3x}\)
câu d
\(D=\dfrac{\left(1-x^2\right)}{x}\left(\dfrac{x^2}{x+3}-1\right)+\dfrac{3x^2-14x+3}{x^2+3x}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\left\{-3;0\right\}\\D=\dfrac{\left(1-x^2\right)\left(x^2-x-3\right)+3x^2-14x+3}{x\left(x+3\right)}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\left\{-3;0\right\}\\D=\dfrac{x^2-x-3-x^4+x^3-3x^2+3x^2-14x+3}{x\left(x+3\right)}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\left\{-3;0\right\}\\D=\dfrac{-x^4+x^3+x^2-15x}{x\left(x+3\right)}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\left\{-3;0\right\}\\D=\dfrac{-x\left(x^3-x^2-x+15\right)}{x\left(x+3\right)}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\left\{-3;0\right\}\\D=\dfrac{-\left(x^3-x^2-x+15\right)}{\left(x+3\right)}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
phân tích ra thừa số nguyên tố
a,6x^2-11x+3 b,2x^2+3x-27 c,2x^2-5xy+3y^2 d,2x^2-5xy-3y^2
e,x^3+2x-3 f,x^3-7x+6 g,x^3+5x^2+8x+4 h,x^3-9x^2+6x+16
j,x^3-x^2-4 k,x^3-x^2-x-2 l,x^3+x^2-x+2 m,x^3-6x^2-x+30
Cho x thỏa mãn \(x^4-6x^2+11x^2-6x+1=0\)
Tính \(A=\frac{2x^2-6x+1}{3x^2-9x-1}\)