CMR:
x2 +y2 - 4x -2y +5 ≥ 0
Tìm tọa độ tâm I của mặt cầu S : x 2 + y 2 + z 2 + 4 x - 2 y + 6 z + 5 = 0
A. I(1;-3;-2)
B. I(-3;-2;1)
C. I(2;-1;3)
D. I(-2;1;-3)
Cho mặt cầu có phương trình x 2 + y 2 + z 2 - 4 x - 2 y + 2 z + 5 = 0 và mặt phẳng P : 3 x - 2 y + 6 z + m = 0 . S và P giao nhau khi
A. 2 ≤ m ≤ 3
B. m > 2 hoặc m < 2
C. - 5 ≤ m ≤ 9
D. m > 9 hoặc m < - 5
Cho mặt cầu (S) có phương trình x 2 + y 2 + z 2 − 4 x − 2 y + 2 z + 5 = 0 và mặt phẳng P : 3 x − 2 y + 6 z + m = 0 . (S) và (P) giao nhau khi
A. m > 3 hoặc m < 2
B. m > 9 hoặc m < -5
C. − 5 ≤ m ≤ 9
D. 2 ≤ m ≤ 3
Cho mặt cầu (S) có phương trình x 2 + y 2 + z 2 -4x -2y+2z+5 = 0 và mặt phẳng
(P): 3x - 2y + 6z + m = 0 và (S) giao nhau khi (P)
![]()
![]()
![]()
![]()
Chọn C
Gọi M(x;y;x). Khi đó M'(x';y';z') là điểm đối xứng

Cho đường tròn (C) có phương trình x 2 + y 2 + 4 x − 2 y − 4 = 0 . Phương trình các tiếp tuyến của đường tròn song song với đường thẳng ∆: x + 2y – 5 = 0 là
A. x + 2 y + 5 ± 3 5 = 0
B. x + 2 y ± 3 = 0
C. x + 2 y ± 3 √ 5 = 0
D. x + 2 y = 0
Các phương trình song song với ∆: x+2y-5=0 có dạng d: x+2y+c=0
Từ đường tròn (C) ta có tâm I(-2;1) và bán kính R=3
Vì đường thẳng d là tiếp tuyến của đường tròn (C) nên ta có:
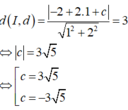
Vậy hai phương trình tiếp tuyến của đường tròn (C) là: x + 2 y + 3 5 = 0 và x + 2 y - 3 5 = 0 .
Tìm tâm và bán kính của các đường tròn sau:
a, x2 + y2– 2x – 2y - 2 = 0
b, 16x2 + 16y2 + 16x – 8y -11 = 0
c, x2 + y2 - 4x + 6y – 3 = 0
Cách 1 : Xác định các hệ số a, b, c.
a) x2 + y2 – 2x – 2y – 2 = 0 có hệ số a = 1 ; b = 1 ; c = –2
⇒ tâm I (1; 1) và bán kính 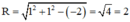
b) 16x2 + 16y2 + 16x – 8y –11 = 0
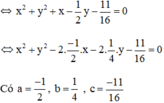
⇒ Đường tròn có tâm 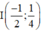 , bán kính
, bán kính 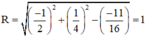
c) x2 + y2 - 4x + 6y - 3 = 0
⇔ x2 + y2 - 2.2x - 2.(-3).y - 3 = 0
có hệ số a = 2, b = -3,c = -3
⇒ Đường tròn có tâm I(2 ; –3), bán kính 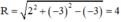
Cách 2 : Đưa về phương trình chính tắc :
a) x2 + y2 - 2x - 2y - 2 = 0
⇔ (x2 - 2x + 1) + (y2 - 2y +1) = 4
⇔(x-1)2 + (y-1)2 = 4
Vậy đường tròn có tâm I(1 ; 1) và bán kính R = 2.
b) 16x2 + 16y2 + 16x - 8y - 11 = 0
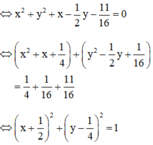
Vậy đường tròn có tâm 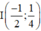 và bán kính R = 1.
và bán kính R = 1.
c) x2 + y2 - 4x + 6y -3 = 0
⇔ (x2 - 4x + 4) + (y2 + 6y + 9) = 4 + 9 + 3
⇔ (x - 2)2 + (y + 3)2 = 16
Vậy đường tròn có tâm I( 2 ; –3) và bán kính R = 4.
Trong không gian Oxyz, cho mặt cầu
S = x 2 + y 2 + z 2 - 4 x - 2 y + 2 z - m 2 - 2 m + 5 = 0
và mặt phẳng α : x + 2 y - 2 z + 3 = 0 . Tìm m để giao tuyến giữa (a) và (S) là một đường tròn
A. m ∈ - 4 ; - 2 ; 2 ; 4
B. m > -2 hoặc m < 4
C. m < -4 hoặc m > -2
D. m < -4 hoặc m > 2
(S) có tâm I(2;1;-1) và bán kính R = m 2 + 2 m + 1 = m + 1
Giao tuyến của (a) và (S) là đường tròn
⇔ d I a < R ⇔ m + 1 > 3 ⇔ m < - 4 m > 2
Đáp án D
a,A=x2+x-2 b,B=4x-x2+5 c,C=9x2-6x+3 d,D=3x+x2-7 e,E=x2+y2-3x+2y+3 f,F=x2+y2-x+4y+5
Lần sau bạn chú ý viết đầy đủ yêu cầu của đề bài.
a) \(A=x^2+x-2=\left(x+2\right)\left(x-1\right)\)
b) \(B=-x^2+4x+5=-\left(x^2-4x-5\right)=-\left(x-5\right)\left(x+1\right)\)
c) \(C=9x^2-6x+3=3\left(3x^2-2x+1\right)\)
Cho mặt cầu S : x 2 + y 2 + z 2 - 4 x + 2 y - 6 z + 5 = 0 và mặt phẳng P : 2 x + 2 y - z + 16 = 0 . Điểm M di động trên (S) và điểm N di động trên (P). Độ dài ngắn nhất của đoạn MN là
A. 2
B. 2
C. 3
D. 0
Vị trí tương đối của hai mặt cầu: x 2 + y 2 + z 2 + 2x - 2y - 2z - 7 = 0 và x 2 + y 2 + z 2 + 2x + 2y + 4z + 5 = 0 là:
A. ở ngoài nhau
B. tiếp xúc
C. cắt nhau
D. chứa nhau
Đáp án C
Mặt cầu: x 2 + y 2 + z 2 + 2x - 2y – 2z – 7 = 0 có tâm I(-1; 1;1) và
Mặt cầu: x 2 + y 2 + z 2 + 2x + 2y + 4z + 5= 0 có tâm I’( -1; -1; -2) và R’ = 1
![]()
Do đó, hai mặt cầu này cắt nhau.