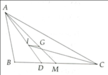
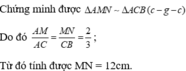Tính độ dài đường phân giác AD của tam giác ABC biết AB=12cm, AC=15cm và BC=18cm.

Những câu hỏi liên quan
Cho tam giác ABC có: AB = 12cm, BC = 15cm, AC = 18cm. Gọi I là giao điểm của các đường phân giác và G là trọng tâm tam giác. Độ dài IG là:
A. 1 cm
B. 2 cm
C. 1,5 cm
D. 2,5 cm
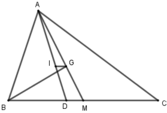
Do M là trung điểm BC nên MB = 1 2 BC = 1 2 .15 = 7,5 cm
Mà BD = 6cm nên DM = 7,5 cm – 6cm = 1,5 cm
Do IG // DM nên I G D M = A G A M = 2 3 => IG = 2 3 DM = 1 3 .1,5 = 1 cm
Đáp án: A
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AC=12cm; BC=15cm
a) Giải tam giác vuông ABC
b) Tính độ dài đường cao AH và đường phân giác AD của tam giác ABC
Cho tam giác ABC có BC = 15cm, AC = 18cm, AB = 12cm. Gọi I và G lần lượt là tâm đường tròn nội tiếp và trọng tâm tam giác ABC.
a) Chứng minh IG song song với BC.
b) Tính độ dài đoạn thẳng IG.
Cho tam giác ABC có các đường phân giác trong BE và CF cắt nhau tại I. Gọi M , N lần lượt là hình chiếu vuông góc của A trên BE và CF. Tia AM cắt BC tại D . Cho AB = 12cm , AC = 15cm và BC = 18cm, tính độ dài đoạn thẳng MN .
Cảm ơn mng nhiều ạ!
1.Cho tam giác ABC có AB=12cm, AC=18cm đường phân giác AD, điểm I thuộc AD sao cho AI=2ID, BI cắt AC tại E
a) Tính tỉ số AE trên EC
b) Tính độ dài AE và EC
a) Xét ΔABC có
AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{BD}{DC}=\dfrac{AB}{AC}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{BD}{DC}=\dfrac{2}{3}\)
\(\Leftrightarrow\dfrac{BD}{2}=\dfrac{CD}{3}\)
mà BD+CD=BC(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{2}=\dfrac{CD}{3}=\dfrac{BD+CD}{2+3}=\dfrac{BC}{5}\)
\(\Leftrightarrow\dfrac{BD}{BC}=\dfrac{2}{5}\)
Kẻ DK//BE(K∈EC)
Xét ΔADK có
I∈AD(gt)
E∈AK(gt)
IE//DK(gt)
Do đó: \(\dfrac{AE}{EK}=\dfrac{AI}{ID}\)(Định lí Ta lét)
hay \(\dfrac{AE}{EK}=2\)
Xét ΔBEC có
D∈BC(gt)
K∈EC(gt)
DK//BE(gt)
Do đó: \(\dfrac{EK}{EC}=\dfrac{BD}{BC}\)(Hệ quả của Định lí Ta lét)
hay \(\dfrac{EK}{EC}=\dfrac{2}{5}\)
Ta có: \(\dfrac{AE}{EK}\cdot\dfrac{EK}{EC}=\dfrac{AE}{EC}\)
\(\Leftrightarrow\dfrac{AE}{EC}=2\cdot\dfrac{2}{5}=\dfrac{4}{5}\)
b) Ta có: \(\dfrac{AE}{EC}=\dfrac{4}{5}\)(cmt)
nên \(\dfrac{AE}{4}=\dfrac{EC}{5}\)
mà AE+EC=AC(E nằm giữa A và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AE}{4}=\dfrac{EC}{5}=\dfrac{AE+EC}{4+5}=\dfrac{18}{9}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{AE}{4}=2\\\dfrac{EC}{5}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AE=2\cdot4=8\left(cm\right)\\EC=2\cdot5=10\left(cm\right)\end{matrix}\right.\)
Vậy: AE=8cm; EC=10cm
Đúng 1
Bình luận (0)
Cho tam giác ABC có: AB 12cm, BC 15cm, AC 18cm. Gọi I là giao điểm của các đường phân giác và G là trọng tâm tam giác. Biết D và M lần lượt là giao điểm của AI, AG với BC. Chọn khẳng định sai: A. IG // BC B.
A
I
I
D
A
G
G
M
C.
A
B...
Đọc tiếp
Cho tam giác ABC có: AB = 12cm, BC = 15cm, AC = 18cm. Gọi I là giao điểm của các đường phân giác và G là trọng tâm tam giác. Biết D và M lần lượt là giao điểm của AI, AG với BC. Chọn khẳng định sai:
A. IG // BC
B. A I I D = A G G M
C. A B G ^ = C B G ^
D. I D A D = M G M A
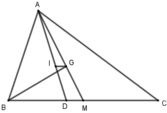
Gọi D, M là giao điểm của AI, AG với BC.
Vì AD là tia phân giác góc B A C ^ nên B D A B = D C A C (t/c)
⇒ B D 12 = D C 18 = B D + D C 12 + 18 = 15 30 = 1 2
=> BD = 12. 1 2 = 6, DC =18. 1 2 = 9
Lại có: BI là tia phân giác A B D ^ nên A I I D = A B B D = 12 6 = 2 (tính chất)
=> I D A D = M G M A = 1 3 hay D đúng
Mà AG = 2GM (vì G là trọng tâm)
Nên A I I D = A G G M = 2 hay B đúng
Theo định lí đảo của định lí Talet ta có:
IG // DM => IG // BC hay A đúng
Chỉ có C sai
Đáp án: C
Đúng 0
Bình luận (0)
Bài 22: Cho tam giác ABC có: AB = 12cm, BC = 15cm, AC = 18cm. Gọi I là giao điểm của các đường phân giác và G là trọng tâm tam giác.
1. Chọn khẳng định sai:
TK
Gọi D, M là giao điểm của AI, AG với BC.
Theo định lí đảo của định lí Talet ta có:
IG // DM ⇒ IG // BC hay A đúng
Chỉ có C sai
Đáp án cần chọn là: C
Đúng 6
Bình luận (0)
1) Cho tam giác ABC cân A, biết cạnh AC = 15cm; BC = 18cm. Tính độ dài các đường cao của tam giác ABC
Nửa chu vi tam giác là (15+15+18)/2=24(cm);
Diện tích tam giác là sqrt[24*(24-15)*(24-15)*(24-18)]=108(cm2);
chiều cao ứng với 2 cạnh bên 15 cm là 108*2/15=14.4(cm);
chiều cao ứng với cạnh đáy 18cm là 108*2/18 =12(cm);
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 12cm, AC = 18cm, BC = 27cm. Điểm D thuộc cạnh BC sao cho CD = 12cm. Tính độ dài AD.
A. 12cm
B. 6cm
C. 10cm
D. 8cm
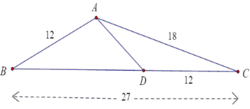
Ta có
A C D C = 18 12 = 3 2 , C B C A = 27 18 = 3 2 ⇒ C A C D = C B C A
Xét ΔACB và ΔDCA có góc C chung và C A C D = C B C A (cmt)
Nên ΔACB ~ ΔDCA (c.g.c)
⇒ A C D C = A B D A ⇔ 3 2 = 12 D A ⇒ D A = 2.12 3 = 8 c m
Đáp án: D
Đúng 0
Bình luận (0)
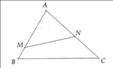
Cho tam giác ABC có AB = 12cm, AC = 15cm, BC = 18cm. Trên cạnh AB, đặt đoạn AM = 10cm trên cạnh AC đặt đoạn AN = 10cm. Tính độ dài đoạn MN