Cho x2+4y2=1. tìm Min, Max: x-y+2018

Những câu hỏi liên quan
cho hai số thực x y thỏa mãn x+y+xy=7/2
tìm min P = x2 +4y2 +4xy
Lời giải:
Áp dụng BĐT AM-GM:
$x^2+2^2\geq 4x$
$4y^2+1\geq 4y$
$\Rightarrow x^2+4y^2+5\geq 4(x+y)$
$\Rightarrow P=x^2+4y^2+4xy\geq 4(x+y)-5+4xy=4(x+y+xy)-5=4.\frac{7}{2}-5=9$
Vậy $P_{\min}=9$. Giá trị này đạt tại $x=2; y=\frac{1}{2}$
Đúng 2
Bình luận (1)
Tìm GTLN (max), GTNN (min) của
y
x
2
-
x
+
2
x
-
1
khi
x
∈
3
2
;
3
Đọc tiếp
Tìm GTLN (max), GTNN (min) của y = x 2 - x + 2 x - 1 khi x ∈ 3 2 ; 3
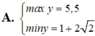
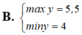
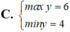
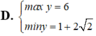
cho x;y thỏa mãn x2+8/x2+y2/8=8 tìm max và min củaB=xy+2024
đúng thì like giúp mik nha bạn. Thx bạn
Đúng 4
Bình luận (5)
1,Cho x,y>0 và xy=2018. Tìm Pmin= 2/x + 1009/y - 2018/(2018x+4y)
2,Cho x,y>0 và x+y=1. Tìm Min B=1/x3+y3 +1/xy
3,Nếu x,y thuộc N* và 2x+3y=53. Tìm max của căn(xy+4)
4,Tìm min P=x^2 +xy +y^2 -3x -3y +2019
5,Cho 0<x<2. Tìm min A= 9x/2-x +2/x
6,Tìm min D= x/y+z + y+z/x + y/x+z + z+x/y + z/x+y + x+y/z
Làm ơn giải giùm mình với, ngay mai kiểm tra rồi.
Cảm ơn nhiều :)))))
Tìm GTLN, GTNN (Max,Min) của
y
x
2
-
3
x
+
3
x
-
2
khi
x
∈
0
;
3
Đọc tiếp
Tìm GTLN, GTNN (Max,Min) của y = x 2 - 3 x + 3 x - 2 khi x ∈ 0 ; 3
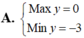
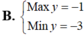

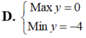
Tìm min hoặc max:
\(^{M=x^2+y^2+xy-3x-3y+2018}\)
\(M=x^2+y^2+xy-3x-3y+2018\)
\(=x^2+2x\frac{\left(y-3\right)}{2}+\left(\frac{y-3}{2}\right)^2+y^2-3y+2018-\left(\frac{y-3}{2}\right)^2\)
\(=\left(x+\frac{y-3}{2}\right)^2+\frac{3y^2-6y+8063}{4}\)
\(=\left(x+\frac{y-3}{2}\right)^2+\frac{3\left(y^2-2y+1\right)}{4}+2015\)
\(=\left(x+\frac{y-3}{2}\right)^2+\frac{3\left(y-1\right)^2}{4}+2015\ge2015\)
\("="\Leftrightarrow x=y=1\)
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất (Min)
x2 + 4y2 + 2023 - 6x - 8y
=x^2-6x+9+4y^2-8y+4+2010
=(x-3)^2+(2y-2)^2+2010>=2010
Dấu = xảy ra khi x=3 và y=1
Đúng 1
Bình luận (0)
Tìm min, max của P = x2 + y2 với x, y là các số thực không âm và x + y + xy = 15
\(\left(x^2+9\right)+\left(y^2+9\right)+3\left(x^2+y^2\right)\ge6x+6y+6xy=90\)
\(\Rightarrow4\left(x^2+y^2\right)+18\ge90\)
\(\Rightarrow x^2+y^2\ge18\)
\(P_{min}=18\) khi \(x=y=3\)
\(x+y+xy=15\Rightarrow\left\{{}\begin{matrix}x\le15\\y\le15\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\left(x-15\right)\le0\\y\left(y-15\right)\le0\end{matrix}\right.\)
\(\Rightarrow x^2+y^2\le15x+15y\) (1)
Cũng từ đó ta có: \(\left(x-15\right)\left(y-15\right)\ge0\Rightarrow xy\ge15x+15y-225\)
\(\Rightarrow16x+16y-225\le x+y+xy=15\)
\(\Rightarrow x+y\le15\) (2)
(1);(2) \(\Rightarrow x^2+y^2\le15.15=225\)
\(P_{max}=225\) khi \(\left(x;y\right)=\left(0;15\right);\left(15;0\right)\)
Đúng 0
Bình luận (0)
cho x;yϵR thỏa mãn x2+y2-xy=4 tìm max và min của C=x2+y2
\(\dfrac{x^2+y^2}{2}\ge xy\Rightarrow-xy\ge-\dfrac{x^2+y^2}{2}\)
\(\Rightarrow4=x^2+y^2-xy\ge x^2+y^2-\dfrac{x^2+y^2}{2}=\dfrac{x^2+y^2}{2}\)
\(\Rightarrow x^2+y^2\le8\)
\(C_{max}=8\) khi \(x=y=\pm2\)
\(x^2+y^2\ge-2xy\Rightarrow-xy\le\dfrac{x^2+y^2}{2}\)
\(4=x^2+y^2-xy\le x^2+y^2+\dfrac{x^2+y^2}{2}=\dfrac{3}{2}\left(x^2+y^2\right)\)
\(\Rightarrow x^2+y^2\ge\dfrac{8}{3}\)
\(C_{min}=\dfrac{8}{3}\) khi \(\left(x;y\right)=\left(-\dfrac{2}{\sqrt{3}};\dfrac{2}{\sqrt{3}}\right);\left(\dfrac{2}{\sqrt{3}};-\dfrac{2}{\sqrt{3}}\right)\)
Đúng 1
Bình luận (1)
 Đúng thì like giúp mik nha bạn. Thx bạn
Đúng thì like giúp mik nha bạn. Thx bạn
Đúng 1
Bình luận (0)
















