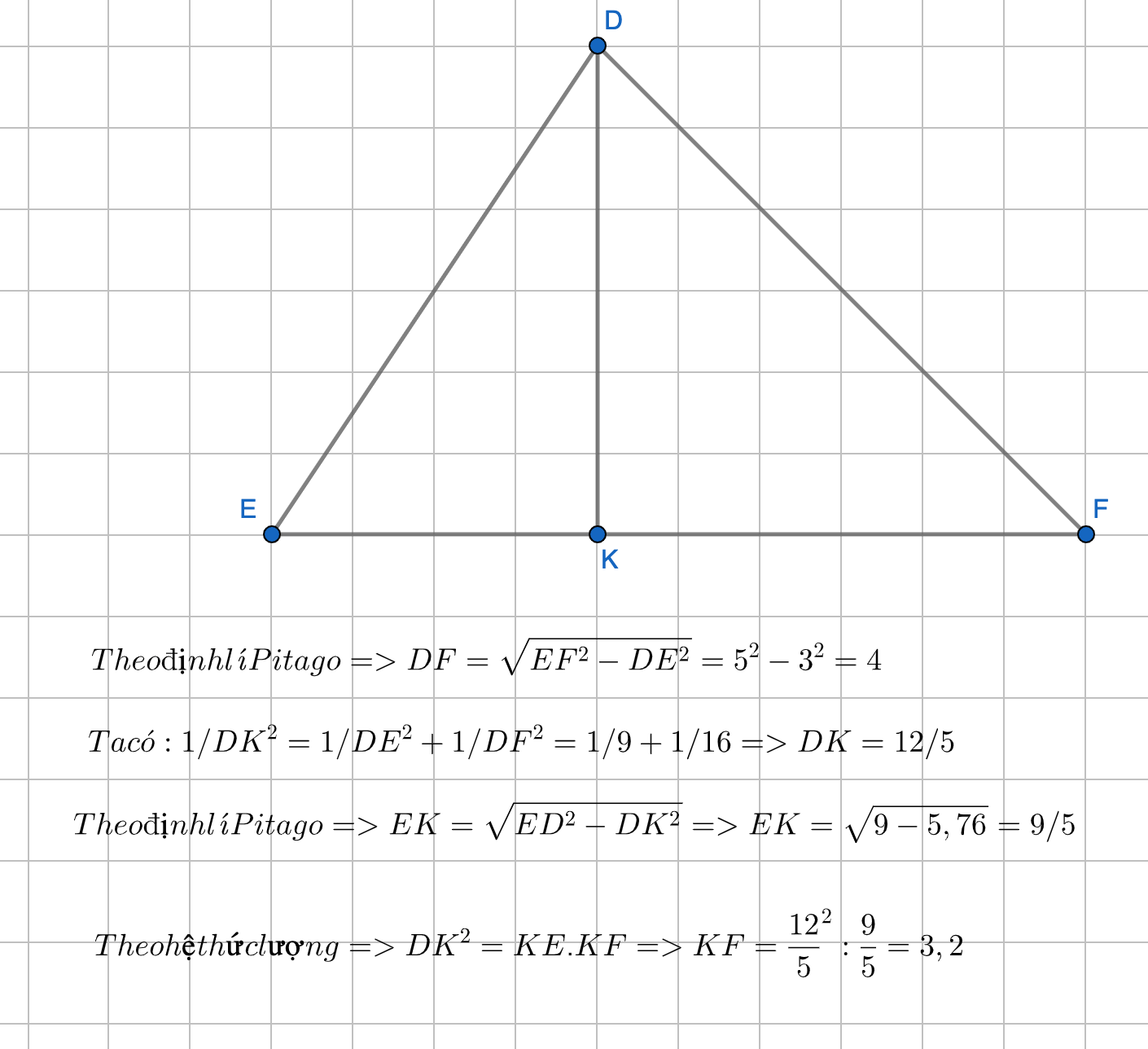
Cho tam giác DEF vuông tại D, đường cao DK . Cho DK = 6cm, EK= 8cm. Tính DE, DF, EF,FK

Những câu hỏi liên quan
Cho tam giác DEF vuông tại D, đường cao DK . Cho DE = 6cm, EK= 8cm. Tính DE, DF, EF,FK
trong ΔDEFΔDEF vuông tại D có
DK2=EK.KFDK2=EK.KF(đlý)⇒KF=DK2EK=628⇒KF=DK2EK=628=4,5
ta có:EF=EK+KF=8+4,5=12,5
DE2=EF.EK(đlý)DE2=EF.EK(đlý)=12,5.8=100⇒DE=10⇒DE=10
DF2=EF.KFDF2=EF.KF(đlý)=12,5.4,5=56,25⇒⇒DF=7,5
Cho tam giác DEF vuông tại D có DE=6cm, DF =8cm, đường cao DH. Đường phân giác EK cắt DH tại I (K ∈ DF)
a) Tính độ dài đoạn thẳng EF,DK,KF
b) Chứng minh △DEK∼△HEI
c) Chứng minh DE.EI=EK.EH
Cho Tam giác DEF biết EF bằng 7,5cm DF bằng 4,5cm DE bằng 6cm a) Tính đường cao DK của tam giác DEF b) Tính EK và FK
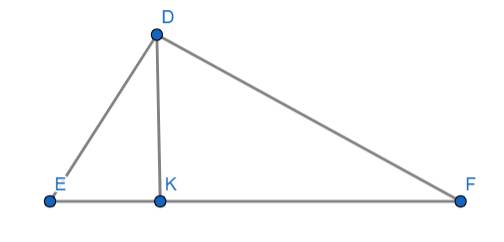
Xét ta có:
\(EF^2=7,5^2=56,25\left(cm\right)\) (1)
Mà: \(DF^2+DE^2=4,5^2+6^2=56,25\left(cm\right)\) (2)
Từ (1) và (2) ta có:
\(EF^2=DE^2+DF^2\)
\(\Rightarrow\Delta DEF\) vuông tại D có đường cao DK
a) Áp dụng hệ thức hai cạnh góc vuông và đường cao ta có:
\(\dfrac{1}{DK^2}=\dfrac{1}{DE^2}+\dfrac{1}{DF^2}\)
\(\Rightarrow DK^2=\dfrac{DE^2DF^2}{DF^2+DF^2}\Rightarrow DK=\sqrt{\dfrac{DE^2DF^2}{DF^2+DE^2}}\)
\(\Rightarrow DK=\sqrt{\dfrac{4,5^2\cdot6^2}{4,5^2+6^2}}=3,6\left(cm\right)\)
b) Áp dụng hệ thức hình chiếu và cạnh góc vuông ta có:
\(\left\{{}\begin{matrix}DE^2=EF\cdot EK\\DF=EF\cdot FK\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}EK=\dfrac{DE^2}{EF}\\FK=\dfrac{DF^2}{EF}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}EK=\dfrac{6^2}{7,5}=4,8\left(cm\right)\\FK=\dfrac{4,5^2}{7,5}=2,7\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
a: Xét ΔDEF có EF^2=DE^2+DF^2
nên ΔDEF vuông tại D
Xét ΔDEF vuông tại D có DK là đường cao
nên DK*FE=DE*DF
=>DE*7,5=27
=>DE=3,6cm
b: ΔDEF vuông tại D có DK là đường cao
nên EK*EF=ED^2
=>EK=6^2/7,5=4,8cm
FK=7,5-4,8=2,7cm
Đúng 0
Bình luận (2)
Cho tam giác DEF , đường cao DK , biết DE=12 cm ,EF=15cm .Tính DF,DK,EK,FK.
Cho tam giác DEF vuông tại D có DE= 6cm, DF= 8 cm, đường cao DH. Đường phân giác EK cắt DH tại I ( K thuộc DF) a) Tính độ dài EF, DK, KF. b) Chứng minh tam giác DEF đồng dạng tam giác HEI => DE. EI= EK. EH c) Gọi G là trung điểm của IK. Chứng minh DG vuông góc với IK
a: \(EF=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xet ΔEDF có EK là phân giác
nên DK/DE=FK/FE
=>DK/3=FK/5=(DK+FK)/(3+5)=8/8=1
=>DK=3cm; FK=5cm
b: Xet ΔDEK vuông tại D và ΔHEI vuông tại H có
góc DEK=góc HEI
=>ΔDEK đồng dạng với ΔHEI
=>ED/EH=EK/EI
=>ED*EI=EK*EH
c: góc DKI=90 độ-góc KED
góc DIK=góc HIE=90 độ-góc KEF
mà góc KED=góc KEF
nên góc DKI=góc DIK
=>ΔDKI cân tại D
mà DG là trung tuyến
nên DG vuông góc IK
Đúng 0
Bình luận (1)
Cho tam giác DEF vuông tại D , có đường cao DK ; DE = 3cm , EF = 5cm . Tính EK , KF , DK.
Áp dụng định lí Pytago vào ΔDEF vuông tại D, ta được:
\(DE^2+DF^2=EF^2\)
\(\Leftrightarrow DF^2=5^2-3^2=16\)
hay DE=4(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔDEF vuông tại D có DK là đường cao ứng với cạnh huyền EF, ta được:
\(DK\cdot FE=DE\cdot DF\)
\(\Leftrightarrow DK\cdot5=3\cdot4=12\)
hay DK=2,4(cm)
Áp dụng định lí Pytago vào ΔDKE vuông tại K, ta được:
\(DE^2=DK^2+EK^2\)
\(\Leftrightarrow EK^2=3^2-2.4^2=3.24\)
hay EK=1,8(cm)
Ta có: EK+FK=EF(K nằm giữa E và F)
nên FK=5-1,8=3,2(cm)
Đúng 3
Bình luận (0)
Áp dụng hệ thức lượng:
\(DE^2=EK.EF\Rightarrow EK=\dfrac{DE^2}{EF}=1,8\left(cm\right)\)
\(KF=EF-EK=3,2\left(cm\right)\)
\(DK^2=EK.KF\Rightarrow DK=\sqrt{EK.KF}=2,4\left(cm\right)\)
Đúng 2
Bình luận (0)
cho tam giác DEf biết DE =6cm ,DF=8cm và Ef=10cm
a)chứng minh DEF là tam giác vuông
B)vẽ đường cao DK hãy tính DK,FK
C)giải tam giác vuông EDK
D)vẽ phân giác trong Em của DEF tính độ dài các đoạn thẳng MD MF ME
giúp mình với mọi người ơi
a: Xét ΔDEF có \(EF^2=DE^2+DF^2\)
nên ΔDEF vuông tại D
b: Xét ΔDEF vuông tại D có DK là đường cao
nên \(\left\{{}\begin{matrix}DK\cdot FE=DE\cdot DF\\DF^2=FK\cdot FE\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}DK=4.8\left(cm\right)\\FK=6.4\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Cho tam giác DEF vuông tại D, đường cao DK . Cho DE = 6cm, EK= 8cm. Tính DK
, DF, EF,FK
trong \(\Delta DEF\) vuông tại D có
\(DK^2=EK.KF\)(đlý)\(\Rightarrow KF=\dfrac{DK^2}{EK}=\dfrac{6^2}{8}\)=4,5
ta có:EF=EK+KF=8+4,5=12,5
\(DE^2=EF.EK\left(đlý\right)\)=12,5.8=100\(\Rightarrow DE=10\)
\(DF^2=EF.KF\)(đlý)=12,5.4,5=56,25\(\Rightarrow\)DF=7,5
Bài 1. vuông tại D, đường cao DK.
1) Biết DE = 12cm, EF = 20cm. Tính EK, FK, DK,DF.
Bài 1. Tam giác DEF vuông tại D, đường cao DK.
1) Biết DE = 12cm, EF = 20cm. Tính EK, FK, DK,DF.
2) Chứng minh : \(\dfrac{DE^2}{EK}=\dfrac{DF^2}{FK}\)
Đúng 0
Bình luận (0)
ta có
tam giác def vuông tại D có đường cao DK nên
DE^2=EK.EF =>EK=DE^2/EF=36/5
FK=EF-EK=64/5
DK^2=EK.FK=2304/25 =>DK=48/5
DF^2=KF.EF=256 =>DF=16
tick mik nha
Đúng 1
Bình luận (0)
1: Áp dụng định lí Pytago vào ΔDEF vuông tại D, ta được:
\(EF^2=DE^2+DF^2\)
\(\Leftrightarrow DF^2=20^2-12^2=256\)
hay DF=16(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔDEF vuông tại D có DK là đường cao ứng với cạnh huyền EF, ta được:
\(\left\{{}\begin{matrix}DK\cdot FE=DE\cdot DF\\DE^2=KE\cdot EF\\DF^2=KF\cdot FE\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}DK=9.6\left(cm\right)\\KE=7.2\left(cm\right)\\KF=12,8\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)