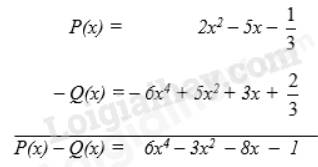Cho đa thức P(x) = 5x \(-\dfrac{1}{2}\)
a) Tính P(-1) ; P(\(-\dfrac{3}{10}\)); b) Tìm nghiệm của đa thức trên

Những câu hỏi liên quan
Bài 5. Cho đa thức P(x) = (5x2+ 5x - 4)(2x2 - 3x + l) - (4x2 - x - 3).
a) Thu gọn và tìm bậc của đa thức P
b) Tính giá trị của đa thức P tại x = \(\dfrac{-1}{2}\).
Mình đang cần gấp
Cho 2 đơn thức
\(A\left(x\right)=-2x^3+11x^2-5x-\dfrac{1}{5}\)
\(B\left(x\right)=2x^3-3x^2-7x+\dfrac{1}{5}\)
a) Tính A(x) + B(x)
b) Tìm đa thức C(x) biết C(x) +B(x) = A(x)
a: \(A\left(x\right)+B\left(x\right)\)
\(=-2x^3+11x^2-5x-\dfrac{1}{5}+2x^3-3x^2-7x+\dfrac{1}{5}\)
\(=8x^2-12x\)
b: C(x)=A(x)-B(x)
\(=-2x^3+11x^2-5x-\dfrac{1}{5}-2x^3+3x^2+7x-\dfrac{1}{5}\)
\(=-4x^3+14x^2+2x-\dfrac{2}{5}\)
Đúng 0
Bình luận (0)
Cho hai đa thức:P(x) 2{x^2} - 5x - dfrac{1}{3}và Q(x) - 6{x^4} + 5{x^2} + dfrac{2}{3} + 3x.Tính hiệu P(x) – Q(x).
Đọc tiếp
Cho hai đa thức:
\(P(x) = 2{x^2} - 5x - \dfrac{1}{3}\)
và \(Q(x) = - 6{x^4} + 5{x^2} + \dfrac{2}{3} + 3x\).
Tính hiệu P(x) – Q(x).
Cho hai đa thức:
\(P\left(x\right)=-2x^4-7x+\dfrac{1}{2}-3x^4+2x^2-x\) ; \(Q\left(x\right)=3x^3+4x^4-5x^2-x^3-6x+\dfrac{3}{2}\)
a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm dần của biến.
b) Tính A(x) = P(x) + Q(x); B(x) = P(x) - Q(x)
a: \(P\left(x\right)=-5x^4+2x^2-8x+\dfrac{1}{2}\)
\(Q\left(x\right)=4x^4+2x^3-5x^2-6x+\dfrac{3}{2}\)
b: \(A\left(x\right)=-5x^4+2x^2-8x+\dfrac{1}{2}+4x^4+2x^3-5x^2-6x+\dfrac{3}{2}=-x^4+2x^3-3x^2-14x+2\)
\(B\left(x\right)=-5x^4+2x^2-8x+\dfrac{1}{2}-4x^4-2x^3+5x^2+6x-\dfrac{3}{2}=-9x^4-2x^3+7x^2-2x-1\)
Đúng 2
Bình luận (0)
a)\(Q\left(x\right)=2x^3+4x^4-6x-5x^2+\dfrac{3}{2}\)
\(P\left(x\right)=2x^2-5x^4-8x+\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
\(A\left(x\right)=2x^3-x^4-3x^2+2-14x\)
\(B\left(x\right)=-2x^3-9x^4-2x+7x^2-1\)
Đúng 1
Bình luận (0)
Bài 5: Cho hai đa thức:
P(x)= \(x^4+2x-6x^2+x^3-5+5x^2\) Q(x)=\(x^4-4x^2-2x+5x^3+1+x^2-6\)
a) Sắp xếp các hạng tử của mỗi đa thức trên theo luỹ thừa giảm dần của biến
b) H(x)=P(x)-Q(x)
c) Tìm bậc của đa thức H(x)
d) Tính H(3);H(-3);H=(\(\dfrac{1}{3}\))
a: \(P\left(x\right)=x^4+x^3-x^2+2x-5\)
\(Q\left(x\right)=x^4+5x^3-3x^2-2x-5\)
b: \(H\left(x\right)=P\left(x\right)-Q\left(x\right)=-4x^3+2x^2+4x\)
c: Bậc của H(x) là 3
Đúng 3
Bình luận (2)
a)\(P\left(x\right)=x^4+x^3-x^2+2x-5\)
\(Q\left(x\right)=x^4+5x^3-3x^2-2x-5\)
b)\(H\left(x\right)=x^4+x^3-x^2+2x-5-x^4-5x^3+3x^2+2x+5\)
\(H\left(x\right)=-4x^3+2x^2+4x\)
c) Bậc : 3
d)\(H\left(3\right)=-4.3^3+2.3^2+4.3=-4.27+2.9+12=-108+18+12=-78\)
\(H\left(-3\right)=-4.\left(-3\right)^3+2.\left(-3\right)^2+4.\left(-3\right)\)
\(H\left(-3\right)=-4.\left(-27\right)+2.9-12=108+18-12=114\)
\(H\left(\dfrac{1}{3}\right)=-4.\left(\dfrac{1}{3}\right)^3+2.\left(\dfrac{1}{3}\right)^2+\dfrac{4.1}{3}=-\dfrac{4.1}{27}+\dfrac{2.1}{9}+\dfrac{4}{3}\)
\(H\left(\dfrac{1}{3}\right)=-\dfrac{4}{27}+\dfrac{6}{27}+\dfrac{36}{27}=\dfrac{38}{27}\)
Đúng 1
Bình luận (0)
BT18: Cho\(P\left(x\right)=5x^2+5x-4\) , \(Q\left(x\right)=2x^2-3x+1\) và \(R\left(x\right)=4x^2-x+3\)
Tính P(x)+Q(x)-R(x) rồi tính giá trị của đa thức tại \(x=-\dfrac{1}{2}\)
`@` `\text {Ans}`
`\downarrow`
`P(x)+Q(x)-R(x)`
`= 5x^2 + 5x - 4 +2x^2 - 3x + 1 - (4x^2 - x + 3)`
`= 5x^2 + 5x - 4 + 2x^2 - 3x + 1 - 4x^2 + x - 3`
`= (5x^2 + 2x^2 - 4x^2) + (5x - 3x + x) + (-4 + 1 - 3)`
`= 3x^2 + 3x - 6`
Thay `x=-1/2`
`3*(-1/2)^2 + 3*(-1/2) - 6`
`= 3*1/4 - 3/2 - 6`
`= 3/4 - 3/2 - 6`
`= -3/4 - 6 = -27/4`
Vậy, khi `x=-1/2` thì GTr của đa thức là `-27/4`
Đúng 4
Bình luận (0)
P(x)+Q(x)-R(x)
=5x^2+5x-4+2x^2-3x+1-4x^2+x-3
=2x^2+3x-6(1)
Khi x=-1/2 thì (1) sẽ là 2*1/4+3*(-1/2)-6=1/2-3/2-6=-7
Đúng 2
Bình luận (1)
Câu 1cho đơn thức Adfrac{1}{5}x^3y.left(-5x^4yz^3right)^2a)Thu gọn A b)xác định hệ số và bậc của Ac)tính giá trị của A tại x2;y1;z-1Câu 2 Cho 2 đa thức P(x)x^5-3x^2+7x^4-9x^3+x^2-dfrac{1}{4}x Q(x)5x^4-x^5+x^2-2x^3+3x^2-dfrac{1}{4}a)hãy sắp sếp các hạng tử của mỗi da thức trên theo lũy thừa giảm dần của biến.b)tính P(x)-Q(x).c)chứng tỏ rằng x0 là nghiệm của da thức P(x) nhưng không phải là nghiệm của đa thức Q(x)mọi người giúp mk 2 câu này cái ạ mk cảm ơn
Đọc tiếp
Câu 1cho đơn thức A=\(\dfrac{1}{5}x^3y.\left(-5x^4yz^3\right)^2\)
a)Thu gọn A
b)xác định hệ số và bậc của A
c)tính giá trị của A tại x=2;y=1;z=-1
Câu 2 Cho 2 đa thức
P(x)=\(x^5-3x^2+7x^4-9x^3+x^2-\dfrac{1}{4}x\)
Q(x)=\(5x^4-x^5+x^2-2x^3+3x^2-\dfrac{1}{4}\)
a)hãy sắp sếp các hạng tử của mỗi da thức trên theo lũy thừa giảm dần của biến.
b)tính P(x)-Q(x).
c)chứng tỏ rằng x=0 là nghiệm của da thức P(x) nhưng không phải là nghiệm của đa thức Q(x)
mọi người giúp mk 2 câu này cái ạ mk cảm ơn
Câu 1 có cần làm không bạn ??? hay chỉ làm câu 2 ??
Đúng 1
Bình luận (1)
Câu 8 :
a , Thu gọn và chỉ ra bậc của đơn thức A=1/2x^3 * 8/5x^2
b , Cho đa thức P(x)=x^2-5x+6
Tính P(0) và P(2)
Câu 9 : Cho 2 đa thức A(x) =5x^3+x^2-3x+5 và B(x)=5x^3+x^2+2x-3
a , Tính A(x)+B(x)
b, Tìm nghiệm của đa thức H(x)= A(x)-B(x) ( giúp vs)
\(Câu8\)
\(a,A=\dfrac{1}{2}x^3\times\dfrac{8}{5}x^2=\left(\dfrac{1}{2}\times\dfrac{8}{5}\right)x^{3+2}=\dfrac{4}{5}x^5\)
b, \(P\left(0\right)=0^2-5.0+6=6\\ P\left(2\right)=2^2-5.2+6=0\)
Câu 9
\(a,A\left(x\right)+B\left(x\right)=5x^3+x^2-3x+5+5x^3+x^2+2x-3\\ =\left(5x^3+5x^3\right)+\left(x^2+x^2\right)+\left(-3x+2x\right)+\left(5-3\right)\\ =10x^3+2x^2-x+2\)
\(b,H\left(x\right)=A\left(x\right)-B\left(x\right)=5x^3+x^2-3x+5-\left(5x^3+x^2+2x-3\right)\\ =5x^3+x^2-3x+5-5x^3-x^2-2x+3\\ =\left(5x^3-5x^3\right)+\left(x^2-x^2\right) +\left(-3x-2x\right)+\left(5+3\right)\\ =-5x+8\)
\(H\left(x\right)=0\\ \Rightarrow-5x+8=0\\ \Rightarrow x=\dfrac{8}{5}\)
vậy nghiệm của đa thức là \(x=\dfrac{8}{5}\)
Đúng 2
Bình luận (0)
Cho đa thức \(P\left(x\right)=\dfrac{5x^3}{4}+\dfrac{5x^2}{6}-\dfrac{21x}{4}+\dfrac{1}{6}\). Tìm số dư khi chia \(P\left(x\right)\) cho \(2x-5\).
Lời giải:
Theo định lý Bê-du về phép chia đa thức, số dư của $P(x)$ khi chia $2x-5$ là $P(\frac{5}{2})=\frac{5}{4}(\frac{5}{2})^3+\frac{5}{6}(\frac{5}{2})^2-\frac{21}{4}.\frac{5}{2}+\frac{1}{6}=\frac{377}{32}$
Đúng 1
Bình luận (0)