Cho biểu thức x4 - 2003x3 + 2003x2 - 2003x + 400 .Tính giá trị bt với x=2002

Những câu hỏi liên quan
cho bt x-y=4 và xy=1 tính giá trị của các biểu thức A=x2+y2,B=x3-y3,C=x4+y4
#Toán lớp 8\(\left\{{}\begin{matrix}x-y=4\\xy=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=y+4\\y\left(y+4\right)=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=y+4\\y^2+4y-1=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=y+4\\\left[{}\begin{matrix}y=-2+\sqrt{5}\\y=-2-\sqrt{5}\end{matrix}\right.\end{matrix}\right.\)
Với \(y=-2+\sqrt{5}\Rightarrow x=2+\sqrt{5}\)
Với \(y=-2-\sqrt{5}\Rightarrow x=2-\sqrt{5}\)
\(\Rightarrow A=x^2+y^2=\left(-2+\sqrt{5}\right)^2+\left(2+\sqrt{5}\right)^2=\left(2-\sqrt{5}\right)^2+\left(-2-\sqrt{5}\right)^2=18\)
\(B=x^3+y^3\Rightarrow\left[{}\begin{matrix}B=\left(2+\sqrt{5}\right)^3+\left(-2+\sqrt{5}\right)^3=34\sqrt{5}\\B=\left(2-\sqrt{5}\right)^3+\left(-2-\sqrt{5}\right)^3=-34\sqrt{5}\end{matrix}\right.\)
\(\Rightarrow C=x^4+y^4=\left(-2+\sqrt{5}\right)^4+\left(2+\sqrt{5}\right)^4=\left(2-\sqrt{5}\right)^4+\left(-2-\sqrt{5}\right)^4=322\)
Đúng 1
Bình luận (0)
Tìm x
(x-5)2=(3+2x)2
27x3-54x2+36x=9
cho bt x-y=4 và xy=1 tính giá trị của các biểu thức A=x2+y2,B=x3-y3,C=x4+y4
a) \(\left(x-5\right)^2=\left(3+2x\right)^2\)
\(\Rightarrow\left(3+2x\right)^2-\left(x-5\right)^2=0\)
\(\Rightarrow\left(3+2x+x-5\right)\left(3+2x-x+5\right)=0\)
\(\Rightarrow\left(3x-2\right)\left(x+8\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}3x-2=0\\x+8=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-8\end{matrix}\right.\)
b) \(27x^3-54x^2+36x=9\)
\(\Rightarrow27x^3-54x^2+36x-9=0\)
\(\Rightarrow27x^3-54x^2+36x-8+8-9=0\)
\(\Rightarrow\left(3x-2\right)^3-1=0\)
\(\Rightarrow\left(3x-2-1\right)\left[\left(3x-2\right)^2+3x-2+1\right]=0\)
\(\Rightarrow\left(3x-3\right)\left[\left(3x-2\right)^2+3x-2+\dfrac{1}{4}-\dfrac{1}{4}+1\right]=0\)
\(\Rightarrow\left(3x-3\right)\left[\left(3x-2+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right]=0\)
\(\Rightarrow\left(3x-3\right)\left[\left(3x-\dfrac{3}{2}\right)^2+\dfrac{3}{4}\right]=0\left(1\right)\)
mà \(\left(3x-\dfrac{3}{2}\right)^2+\dfrac{3}{4}>0,\forall x\)
\(\left(1\right)\Rightarrow3x-3=0\Rightarrow3x=3\Rightarrow x=1\)
Đúng 2
Bình luận (0)
(\(x-5\))2 = (3 +2\(x\))2 ⇒ \(\left[{}\begin{matrix}x-5=3+2x\\x-5=-3-2x\end{matrix}\right.\) ⇒ \(\left[{}\begin{matrix}x=-8\\x=\dfrac{2}{3}\end{matrix}\right.\) vậy \(x\in\){-8; \(\dfrac{2}{3}\)}
27\(x^3\) - 54\(x^2\) + 36\(x\) = 9
27\(x^3\) - 54\(x^2\) + 36\(x\) - 8 = 1
(3\(x\) - 2)3 = 1 ⇒ 3\(x\) - 2 = 1 ⇒ \(x\) = 1
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Cho biểu thức A=\(\frac{2002x+1}{2003x-2003}\)với x khác 1
Tìm số nguyên x để A đạt giá trị lớn nhất ? tìm giá trị lớn nhất đó
\(A=\frac{2002\left(x-1\right)+2003}{2003\left(x-1\right)}=\frac{2002}{2003}+\frac{1}{x-1}\)
=> x-1 phải là sô nguyên dương nhỏ nhất => x-1=1=> x=2
Đúng 0
Bình luận (0)
Cho x+y=4 và x2+y2=10. Tính giá trị của biểu thức M=x6+y6
Cho 8x3-32y-32x2y+8x=0 và y khác 0. Tính giá trị của biểu thức M=3x+2y/3x-2y
Cho x2-5x+1=0 . Tính giá trị của biểu thức M=x4+x21/2x2
Giải giúp mình với!!!
Bài 1:
$2xy=(x+y)^2-(x^2+y^2)=4^2-10=6\Rightarrow xy=3$
$M=x^6+y^6=(x^3+y^3)^2-2x^3y^3$
$=[(x+y)^3-3xy(x+y)]^2-2(xy)^3=(4^3-3.3.4)^2-2.3^3=730$
Đúng 2
Bình luận (0)
Bài 2:
$8x^3-32y-32x^2y+8x=0$
$\Leftrightarrow (8x^3+8x)-(32y+32x^2y)=0$
$\Leftrightarrow 8x(x^2+1)-32y(1+x^2)=0$
$\Leftrightarrow (8x-32y)(x^2+1)=0$
$\Rightarrow 8x-32y=0$ (do $x^2+1>0$ với mọi $x$)
$\Leftrightarrow x=4y$
Khi đó:
$M=\frac{3.4y+2y}{3.4y-2y}=\frac{14y}{10y}=\frac{14}{10}=\frac{7}{5}$
Đúng 2
Bình luận (0)
Bài cuối $x^21$ không rõ. Bạn xem lại.
Đúng 1
Bình luận (0)
Tìm x
(x-5)^2=(3+2x)^2
27x^3-54x^2+36x=9
cho bt x-y=4 và xy=1 tính giá trị của các biểu thức A=x2+y2,B=x3-y3,C=x4+y4
(x - 5)² = (3 + 2x)²
(x - 5)² - (3 + 2x)² = 0
[(x - 5) - (3 + 2x)][(x - 5) + (3 + 2x)] = 0
(x - 5 - 3 - 2x)(x - 5 + 3 + 2x) = 0
(-x - 8)(3x - 2) = 0
-x - 8 = 0 hoặc 3x - 2 = 0
*) -x - 8 = 0
-x = 8
x = -8
*) 3x - 2 = 0
3x = 2
x = 2/3
Vậy x = -8; x = 2/3
--------------------
27x³ - 54x² + 36x = 9
27x³ - 54x² + 36x - 9 = 0
27x³ - 27x² - 27x² + 27x + 9x - 9 = 0
(27x³ - 27x²) - (27x² - 27x) + (9x - 9) = 0
27x²(x - 1) - 27x(x - 1) + 9(x - 1) = 0
(x - 1)(27x² - 27x + 9) = 0
x - 1 = 0 hoặc 27x² - 27x + 9 = 0
*) x - 1 = 0
x = 1
*) 27x² - 27x + 9 = 0
Ta có:
27x² - 27x + 9
= 27(x² - x + 1/3)
= 27(x² - 2.x.1/2 + 1/4 + 1/12)
= 27[(x - 1/2)² + 1/12] > 0 với mọi x ∈ R
⇒ 27x² - 27x + 9 = 0 (vô lí)
Vậy x = 1
Đúng 1
Bình luận (0)
A = x² + y²
= x² - 2xy + y² + 2xy
= (x - y)² + 2xy
= 4² + 2.1
= 16 + 2
= 18
B = x³ - y³
= (x - y)(x² + xy + y²)
= (x - y)(x² - 2xy + y² + xy + 2xy)
= (x - y)[(x - y)² + 3xy]
= 4.(4² + 3.1)
= 4.(16 + 3)
= 4.19
= 76
C = x⁴ + y⁴
= (x²)² + (y²)²
= (x²)² + 2x²y² + (y²)² - 2x²y²
= (x² + y²)² - 2x²y²
= (x² - 2x²y² + y² + 2x²y²)² - 2x²y²
= [(x - y)² + 2x²y²]² - 2x²y²
= (4² + 2.1²)² - 2.1²
= (16 + 2)² - 2
= 18² - 2
= 324 - 2
= 322
Đúng 1
Bình luận (0)
a: =>(2x+3)^2-(x-5)^2=0
=>(2x+3+x-5)(2x+3-x+5)=0
=>(x+8)(3x-2)=0
=>x=2/3 hoặc x=-8
b: =>27x^3-54x^2-36x-9=0
=>3x^3-6x^2-4x-1=0
=>\(x\simeq2,57\)
c: A=x^2+y^2=(x-y)^2+2xy=4^2+2=18
B=x^3-y^3=(x-y)^3+3xy(x-y)
=4^3+3*1*4
=64+12=76
C=(x^2+y^2)^2-2x^2y^2
=18^2-2*1^2=322
Đúng 0
Bình luận (0)
Tính giá trị của biểu thức B = x 4 - 2 x 3 2 x 2 - x 3 với x = - 1 2
Điều kiện xác định của phân thức: x ≠ 0, x ≠ 2
Ta có 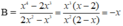
Với x = - thỏa mãn điều kiện xác định của phân thức ⇒ B =
thỏa mãn điều kiện xác định của phân thức ⇒ B = 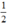
Đúng 0
Bình luận (0)
a/ Tìm a sao cho đa thức : x4 – x3 + 6x2 – x + a chia hết cho đa thức: x2 – x + 5
b/ Tính giá trị nguyên của n để giá trị của biểu thức : 3n3 + 10n2 – 5 chia hết cho giá trị của biểu thức: 3n + 1
b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)
Đúng 1
Bình luận (0)
Cho x-15=-16
Và \(17-|y|=\frac{5^2-5^{-1}-\left(2004^0\right)^{2003}}{2^{-2}}\)
Tính giá trị của \(A=2003x^{2002}-2004y^{2003}\)
thu gọn rồi tính giá trị
2003x100+2003x99+.....+2003x2+2003x
tại x=2004
A=2003x(1+x+x2+...+x98+x99)
=> \(\frac{A}{2003x}=1+x+x^2+...+x^{98}+x^{99}\)
=> \(\frac{A.x}{2003x}=x+x^2+...+x^{98}+x^{99}+x^{100}\)=> \(\frac{A}{2003}=x+x^2+...+x^{98}+x^{99}+x^{100}\)
=> \(\frac{A}{2003}-\frac{A}{2003x}=\left(x+x^2+...+x^{98}+x^{99}+x^{100}\right)-\left(1+x+x^2+...+x^{98}+x^{99}\right)\)
=> \(\frac{A\left(x-1\right)}{2003x}=x^{100}-1\)=> \(A=\frac{2003x\left(x^{100}-1\right)}{x-1}\)
Thay x=2004 ta được: \(A=\frac{2003.2004\left(2004^{100}-1\right)}{2004-1}=2004\left(2004^{100}-1\right)\)
Đáp số: \(A=2004\left(2004^{100}-1\right)\)
Đúng 0
Bình luận (0)






















