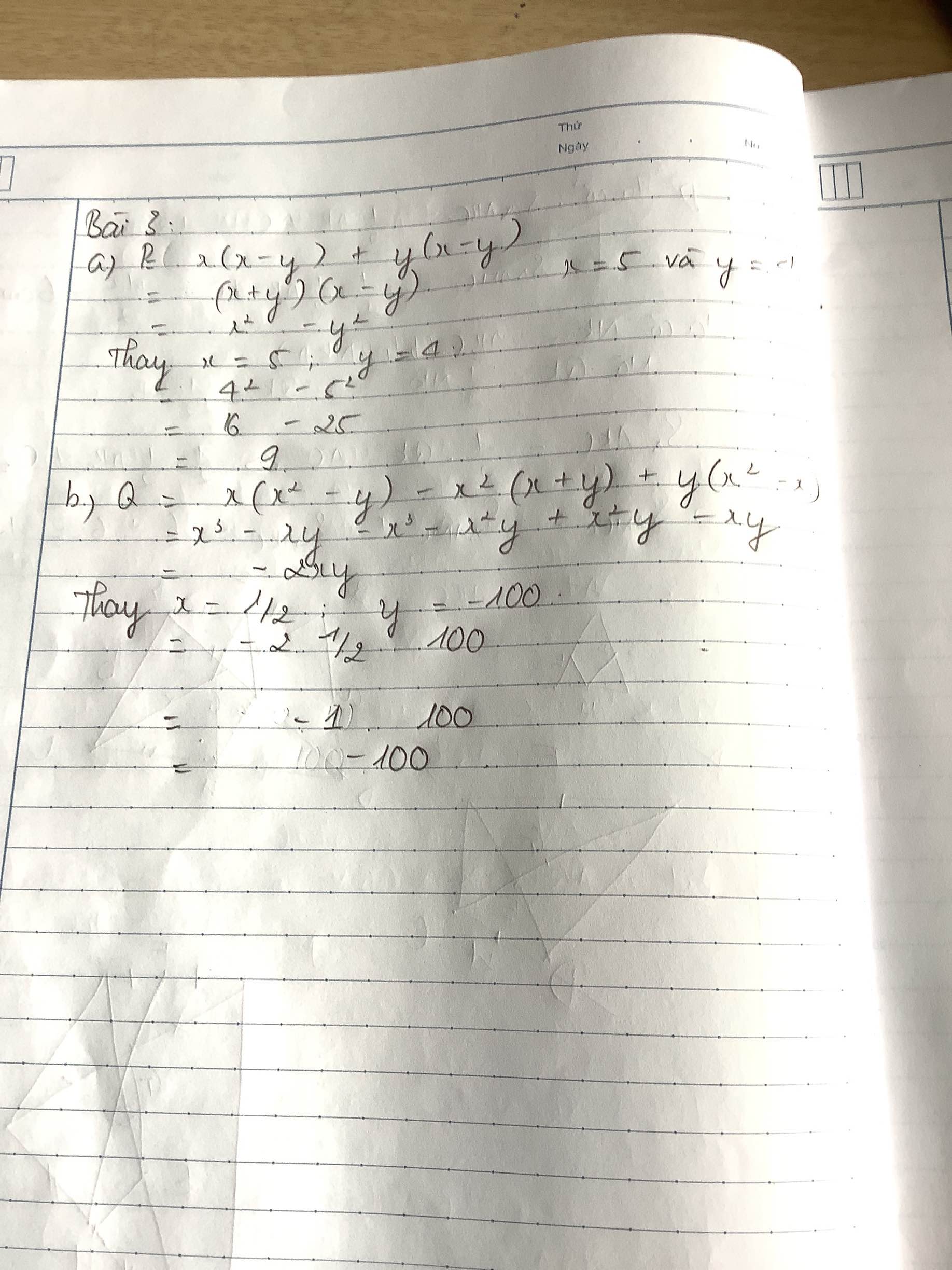Lời giải:
a)

$x(x-y)+y(x+y)=x^2-xy+xy+y^2=x^2+y^2=(-6)^2+(-5)^2=61$

b)

$x(x^2-y)-x^2(x+y)+y(x^2-x)=x^3-xy-x^3-x^2y+x^2y-xy$

$=-2xy=-2.\frac{1}{2}.(-100)=100$

a) Tìm được A = (x- y)(x + 5y).

Thay x = 4 và y = -4 vào A tìm được A = -128.

b) Tìm được B = 9 ( x   - 1 ) 2 .

Thay x = - 4 vào B tìm được B = 81 4 .  

c) Tìm được C = (x - y)(y - z)(x - z).

Thay x = 6,y = 5 và z = 4 vào C tìm được C = 2.

d) Thay 10 = x +1 vào D và biến đổi ta được D = -1.

a.\(x=0;y=-1\)

\(\Rightarrow2.0-\dfrac{-1\left(0^2-2\right)}{0.-1-1}=0-\dfrac{2}{-1}=2\)

b.\(x=2\)

\(\Rightarrow4.2^2-3\left|2\right|-2=16-6-2=8\)

\(x=-3\)

\(\Rightarrow4.\left(-3\right)^2-3\left|-3\right|-2=36-9-2=25\)

c.\(x=-\dfrac{1}{5};y=-\dfrac{3}{7}\)

\(\Rightarrow5.\left(-\dfrac{1}{5}\right)^2-7.\left(-\dfrac{3}{7}\right)+6=5.\dfrac{1}{25}+3+6=\dfrac{1}{5}+3+6=\dfrac{46}{5}\)

thay x=2 và biểu thức A ta đc

\(A=4.2^2-3.\left|2\right|-2=4.4-6-2=16-6-2=8\)

thay x=-3  biểu thức A ta đc

\(A=4.\left(-3\right)^2-3.\left|-3\right|-2=4.9-9-2=36-9-2=25\)

thay x=-1/5 ; y=-3/7  biểu thức B ta đc

\(B=5.\left(-\dfrac{1}{5}\right)^2-7.\left(-\dfrac{3}{7}\right)+6\)

\(B=5\cdot\dfrac{1}{25}+3+6\)

\(B=\dfrac{1}{5}+3+6=\dfrac{46}{5}\)

 thay x =0 , y= -1 và biểu thức ta  đc

\(0-\dfrac{\left(-1\right)\left(0^2-2\right)}{0.\left(-1\right)+\left(-1\right)}=0-\dfrac{2}{-1}=0+2=2\)

a) M = (x² + 3xy - 3x³) + (2y³ - xy + 3x³)

= x² + 3xy - 3x³ + 2y³ - xy + 3x³

= x² + (3xy - xy) + (-3x³ + 3x³) + 2y³

= x² + 2xy + 2y³

Tại x = 5 và y = 4

M = 5² + 2.5.4 + 2.4³

= 25 + 40 + 2.64

= 65 + 128

= 193

b) N = x²(x + y) - y(x² - y²)

= x³ + x²y - x²y + y³

= x³ + (x²y - x²y) + y³

= x³ + y³

Tại x = -6 và y = 8

N = (-6)³ + 8³

= -216 + 512

= 296

c) P = x² + 1/2 x + 1/16

= (x + 1/2)²

Tại x = 3/4 ta có:

P = (3/4 + 1/2)² = (5/4)² = 25/16

a) \(=x^2-xy+xy+y^2=x^2+y^2\)tự thay rồi tính nha

b) \(=x^3-xy-x^3-x^2y+x^2y-xy=-2xy\) tự thay vào nha

a) x(x – y) + y (x + y) = x² – xy +yx + y²= x²+ y²

với x = -6, y = 8 biểu thức có giá trị là (-6)² + 8² = 36 + 64 = 100

b) x(x² – y) – x² (x + y) + y (x²– x) = x³ – xy – x³ – x²y + yx² – yx= (2x-2y) – (x² -2xy +y²) =2(x-y) – (x-y)²

Với x =1/2, y = -100 biểu thức có giá trị là -2 . 1/2. (-100) = 100.

\(x\left(x-y\right)+y\left(x+y\right)\)

\(=x^2-xy+xy+y^2\)

\(=x^2+y^2\)

Tại \(x=-6;y=8\)thì biểu thức có giá trị là:

\(\left(-6\right)^2+8^2=100\)

\(x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)\)

\(=x^3-xy-x^3-x^2y+x^2y-xy\)

\(=-2xy\)

Tại \(x=\frac{1}{2};y=100\)

\(-2.\frac{1}{2}.100=-100\)

a ) 

Thay x = -6 và y = 8 vào phương trình , ta có : 

-6.( -6 -8 ) + 8.(-6+8 ) 

=36 + 48   - 48     + 64 

= 36 + 64 

=  100 

a) x ( x - y ) + y ( x + y )

= x² - xy + xy + y²

= x² + y²

Thay x = -6 và y = 8 , ta được :

( -6 )² + 8² = 36 + 64 = 100

b) x ( x² - y ) - x² - x² ( x + y ) + y ( x² - x )

= x³ - xy - x² - x³ - x²y + x²y - xy

= ( x³ - x³ ) - ( xy + xy ) - ( x²y - x²y ) - x²

= -2xy - x²

\(A=x\left(x-y\right)+y\left(x+y\right)\)

\(=x^2-xy+xy+y^2\)

\(=x^2+y^2\)

Thay x = -6;  y = 8 vào ta đc

\(A=\left(-6\right)^2+8^2=100\)

a) \(P=x\left(x-y\right)+y\left(x-y\right)=\left(x-y\right)\left(x+y\right)=x^2-y^2=5^2-4^2=9\)

b) \(Q=x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)=x^3-xy-x^3-x^2y+x^2y-xy=0\)