Viết phương trình tính tống S=\(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+...+\dfrac{1}{2n}\)
Tính tổng: a) \(S=2C^2_{2n}+4C^4_{2n}+6C^6_{2n}+...+2nC^{2n}_{2n}\)
b) \(S=\dfrac{1}{2}C^0_{2n}+\dfrac{1}{4}C^2_{2n}+\dfrac{1}{6}C^4_{2n}+...+\dfrac{1}{2n+2}C^{2n}_{2n}\)
Viết chương trình tính tổng :
1, S= \(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+....+\dfrac{1}{2n}\)
2,S= \(\dfrac{1}{1!}+\dfrac{1}{2!}+\dfrac{1}{3!}+...+\dfrac{1}{n!}\)
program Bai_1;
uses crt;
var n,i:integer; s:real;
begin
clrscr;
write('Nhap n: '); readln(n);
for i:=1 to n do s:=s+1/(2*i);
write('S=',s);
readln;
end.
program Bai_2;
uses crt;
var n,i:integer; gt:longint; s:real;
begin
clrscr;
write('n='); readln(n);
gt:=1;
for i:=1 to n do
begin
gt:=gt*i;
s:=s+1/gt;
end;
write('S=',s);
readln;
end.
a, Tính: M = \(1+\dfrac{1}{5}+\dfrac{3}{35}+...+\dfrac{3}{9603}+\dfrac{3}{9999}\)
b, Chứng tỏ: S = \(\dfrac{1}{4^2}+\dfrac{1}{6^2}+\dfrac{1}{8^2}+...+\dfrac{1}{\left(2n\right)^2}< \dfrac{1}{4}\left(n\in N,n\ge2\right)\)
a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)
b: 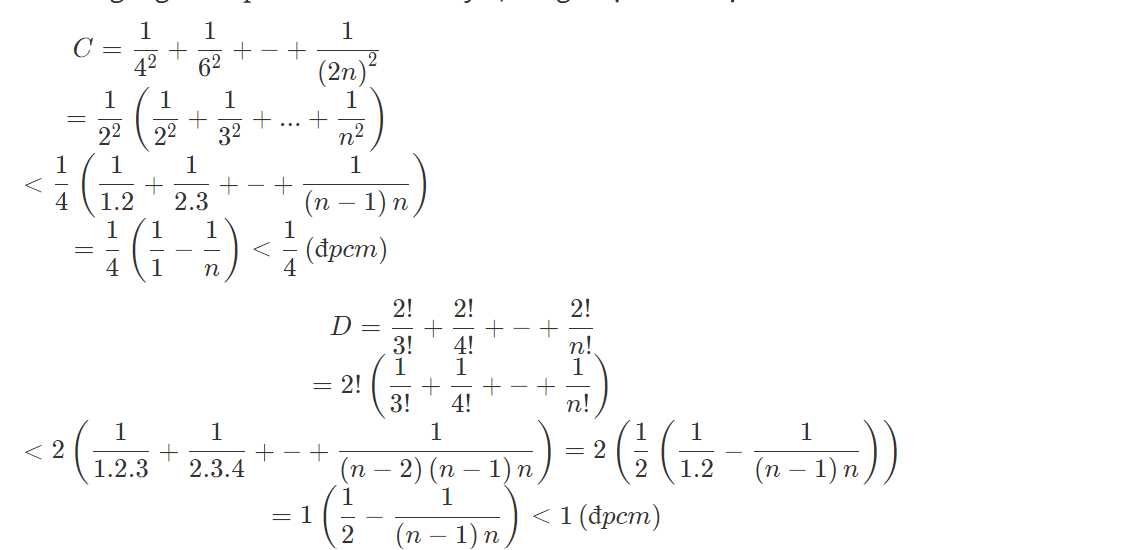
Viết thuật toán liệt kê hoặc sơ đồ khối:
Tính \(S=\dfrac{1}{2}+\dfrac{3}{4}+\dfrac{5}{6}+...+\dfrac{2n+1}{2n+2}\)
chứng minh rằng \(S=\dfrac{1}{4^2}+\dfrac{1}{6^2}+\dfrac{1}{8^2}+...+\dfrac{1}{\left(2n\right)^2}< \dfrac{1}{4}\left(n\in N,n\ge2\right)\)
\(S=\dfrac{1}{2^2}\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}\right)\)
=>\(S< =\dfrac{1}{4}\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n-1}-\dfrac{1}{n}\right)\)
=>\(S< =\dfrac{1}{4}\cdot\left(1-\dfrac{1}{n}\right)=\dfrac{1}{4}\cdot\dfrac{n-1}{n}< =\dfrac{1}{4}\)
a)Tính tổng\(P=\dfrac{1}{1+2}+\dfrac{1}{1+2+3}+\dfrac{1}{1+2+3+4}+...+\dfrac{1}{1+2+3+...+2017}\)
b)CMR\(\dfrac{1}{4^2}+\dfrac{1}{6^2}+\dfrac{1}{8^2}+...+\dfrac{1}{\left(2n\right)^2}< \dfrac{1}{4}\)
\(a,P=\dfrac{1}{\left(2+1\right)\left(2+1-1\right):2}+\dfrac{1}{\left(3+1\right)\left(3+1-1\right):2}+...+\dfrac{1}{\left(2017+1\right)\left(2017+1-1\right):2}\\ P=\dfrac{1}{2\cdot3:2}+\dfrac{1}{3\cdot4:2}+...+\dfrac{1}{2017\cdot2018:2}\\ P=2\left(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2017\cdot2018}\right)\\ P=2\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2017}-\dfrac{1}{2018}\right)\\ P=2\left(\dfrac{1}{2}-\dfrac{1}{2018}\right)=2\cdot\dfrac{504}{1009}=\dfrac{1008}{1009}\)
\(b,\) Ta có \(\dfrac{1}{4^2}< \dfrac{1}{2\cdot4};\dfrac{1}{6^2}< \dfrac{1}{4\cdot6};...;\dfrac{1}{\left(2n\right)^2}< \dfrac{1}{\left(2n-2\right)2n}\)
\(\Leftrightarrow VT< \dfrac{1}{2\cdot4}+\dfrac{1}{4\cdot6}+...+\dfrac{1}{\left(2n-2\right)2n}\\ \Leftrightarrow VT< \dfrac{1}{2}\left(\dfrac{2}{2\cdot4}+\dfrac{2}{4\cdot6}+...+\dfrac{2}{\left(2n-2\right)2n}\right)\\ \Leftrightarrow VT< \dfrac{1}{2}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{2n-2}-\dfrac{1}{2n}\right)\\ \Leftrightarrow VT< \dfrac{1}{2}\left(1-\dfrac{1}{2n}\right)< \dfrac{1}{2}\cdot\dfrac{1}{2}=\dfrac{1}{4}\)
Viết chương trình tính \(S=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{n}+...\)cho đến khi S>a với a là một số cho trước ,n là một số nguyên dương
1. Viết chương trình tính tổng sau:
a) S = \(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{n}\)
b) S = \(1+\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{n}\)
2. Viết chương trình nhập 2 số nguyên a và b. Tìm bội chung nhỏ nhất
3. Cho một dãy số gồm N phân tử:
- Tính tổng các phân tử trong dãy số
- Tìm phân tử lớn nhất
- In ra màn hình các số nguyên tố có trong dãy
BÀI 3
uses crt;
var a: array[1..100] of integer;
i,n,max,s,j: integer;
begin
clrscr;
writeln(' nhap so phan tu cua day'); readln(n);
for i:=1 to n do
begin
writeln('a[',i,']'); readln(a[i]);
end;
max:=a[1];
s:=0;
for i:=1 to n do
begin
if max<a[i] then max:=a[i];
s:=s+a[i];
end;
writeln('so lon nhat trong day tren la:',max);
writeln('tong bang:',s);
writeln('so nguyen to trong mang la:');
j:=1;
for i:=1 to n do
if a[i]>1 then
begin
repeat
inc(j);
until (a[i] mod j=0);
if j>(a[i] div 2) then writeln(a[i]);
j:=1;
end;
readln
end.
1. Viết chương trình yêu cầu nhập số nguyên N từ bàn phím. Tính tổng các số nguyên đầu tiên của N theo công thức S= \(\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{7}...+\dfrac{1}{2N+1}\)(với N \(\ge\)1). Sau đó in kết quả ra màn hình.
2. Cho dãy số sau: 2; 5; 8; 11. Viết chương trình yêu cầu nhập số nguyên N từ bàn phím. Tính tích E, sau đó in ra màn hình.
E= 2.5.8.11.. } N số nguyên
Bài 1:
uses crt;
var n,i:integer;
s:real;
begin
clrscr;
write('Nhap n='); readln(n);
s:=0;
for i:=1 to n do
s:=s+1/(2*i+1);
writeln(s:4:2);
readln;
end.