chứng tỏ rằng với a, b là các số bất kì thì a2+b2+2≥2(a+b)

Những câu hỏi liên quan
Chứng tỏ rằng với a và b là các số bất kì thì: a 2 + b 2 / 2 ≥ a b
Ta có: a - b 2 ≥ 0 ⇒ a 2 + b 2 - 2 a b ≥ 0
⇒ a 2 + b 2 - 2 a b + 2 a b ≥ 2 a b ⇒ a 2 + b 2 ≥ 2 a b
⇒ a 2 + b 2 . 1 / 2 ≥ 2 a b . 1 / 2 ⇒ a 2 + b 2 / 2 ≥ a b
Đúng 0
Bình luận (0)
Chứng tỏ rằng với a và b là các số bất kì thì: a 2 + b 2 - 2 a b ≥ 0
Ta có: a - b 2 ≥ 0 ⇒ a 2 + b 2 - 2 a b ≥ 0
Đúng 0
Bình luận (0)
chứng tỏ rằng với a và b là các số bất kì thì: a2 +b2 -2ab lớn hơn hoặc bằng 0
Trả lời
a^2 + b^2 - 2ab
= ( a^2 - 2ab + b^2 )
= ( a - b )^2 ≥ 0 ( luôn đúng )
Vậy...
Đúng 0
Bình luận (0)
\(a^2+b^2-2ab=\left(a-b\right)^2\ge\forall a,b\)
Đúng 0
Bình luận (0)
Hằng đẳng thức số 2 \(a^2-2ab+b^2=\left(a-b\right)^2\)
\(\Rightarrow\left(a-b\right)^2\ge0\)
Vậy \(a^2+b^2-2ab\ge0\left(đpcm\right)\)
Đúng 0
Bình luận (0)
với a b c là 3 số bất kì cm a2+b2+c2+3≥2(a+b+c)
Ta có:
\(\left(a-1\right)^2\ge0;\forall a\) (1)
\(\left(b-1\right)^2\ge0;\forall b\) (2)
\(\left(c-1\right)^2\ge0;\forall c\) (3)
Cộng từng vế (1);(2);(3) ta được:
\(\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2\ge0\)
\(\Leftrightarrow a^2-2a+1+b^2-2b+1+c^2-2c+1\ge0\)
\(\Leftrightarrow a^2+b^2+c^2-2\left(a+b+c\right)+3\ge0\)
\(\Leftrightarrow a^2+b^2+c^2+3\ge2\left(a+b+c\right)\) ( đfcm )
Đúng 1
Bình luận (0)
Ta có:
(a−1)2≥0;∀a(a−1)2≥0;∀a (1)
(b−1)2≥0;∀b(b−1)2≥0;∀b (2)
(c−1)2≥0;∀c(c−1)2≥0;∀c (3)
Cộng từng vế (1);(2);(3) ta được:
(a−1)2+(b−1)2+(c−1)2≥0(a−1)2+(b−1)2+(c−1)2≥0
⇔a2−2a+1+b2−2b+1+c2−2c+1≥0⇔a2−2a+1+b2−2b+1+c2−2c+1≥0
⇔a2+b2+c2−2(a+b+c)+3≥0⇔a2+b2+c2−2(a+b+c)+3≥0
⇔a2+b2+c2+3≥2(a+b+c)⇔a2+b2+c2+3≥2(a+b+c) ( đpcm ).
Đúng 0
Bình luận (0)
Giả sử `a^2+b^2+c^2+3ge2.(a+b+c)`
`<=>a^2+b^2+c^2+3ge2a+2b+2c`
`<=>a^2+b^2+c^2+3-2a-2b-2cge0`
`<=>(a^2-2a+1)+(b^2-2b+1)+(c^2-2c+1)ge0`
`<=>(a-1)^2+(b-1)^2+(c-1)^2ge0(text{luôn đúng})`
Dấu `=` xảy ra khi:`a=b=c=1`
Đúng 1
Bình luận (0)
Với a, b là hai số bất kì, trong các đẳng thức sau, đẳng thức nào không phải hằng đẳng
thức?
A. (a+b)2 =a2 +2ab+b2 B. a2 – 1 =3a C. a(2a+b) =2a2 + ab D. a(b+c) =ab+ac
Câu 29. Chứng minh các bất đẳng thức:a) (a + b)2 ≤ 2(a2 + b2)b) (a + b + c)2 ≤ 3(a2 + b2 + c2)c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).Câu 30. Cho a3 + b3 2. Chứng minh rằng a + b ≤ 2.Câu 31. Chứng minh rằng: [x] + [y] ≤ [x + y].Câu 32. Tìm giá trị lớn nhất của biểu thức: Câu 33. Tìm giá trị nhỏ nhất của: với x, y, z 0.Câu 36. Xét xem các số a và b có thể là số vô tỉ không nếu:a) ab và a/b là số vô tỉ.b) a + b và a/b là số hữu tỉ (a + b ≠ 0)c) a + b, a2 và b2 là số hữu tỉ (a + b ≠...
Đọc tiếp
Câu 29. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
Câu 30. Cho a3 + b3 = 2. Chứng minh rằng a + b ≤ 2.
Câu 31. Chứng minh rằng: [x] + [y] ≤ [x + y].
Câu 32. Tìm giá trị lớn nhất của biểu thức: ![]()
Câu 33. Tìm giá trị nhỏ nhất của: ![]() với x, y, z > 0.
với x, y, z > 0.
Câu 36. Xét xem các số a và b có thể là số vô tỉ không nếu:
a) ab và a/b là số vô tỉ.
b) a + b và a/b là số hữu tỉ (a + b ≠ 0)
c) a + b, a2 và b2 là số hữu tỉ (a + b ≠ 0)
Câu 37. Cho a, b, c > 0. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 38. Cho a, b, c, d > 0. Chứng minh:
![]()
Câu 39. Chứng minh rằng [2x] bằng 2[x] hoặc 2[x] + 1
Câu 40. Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
Câu 41. Tìm các giá trị của x để các biểu thức sau có nghĩa:
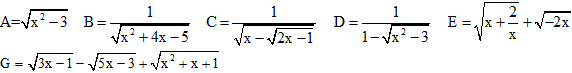 Mn giúp em với ;-;
Mn giúp em với ;-;
1 Cho biểu thức M a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.2 Chứng minh các bất đẳng thức:a) (a + b)2 ≤ 2(a2 + b2)b) (a + b + c)2 ≤ 3(a2 + b2 + c2)c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).3 Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
Đọc tiếp
1 Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
2 Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
3 Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
2:
a: =>a^2+2ab+b^2-2a^2-2b^2<=0
=>-(a^2-2ab+b^2)<=0
=>(a-b)^2>=0(luôn đúng)
b; =>a^2+b^2+c^2+2ab+2ac+2bc-3a^2-3b^2-3c^2<=0
=>-(2a^2+2b^2+2c^2-2ab-2ac-2bc)<=0
=>(a-b)^2+(b-c)^2+(a-c)^2>=0(luôn đúng)
Đúng 1
Bình luận (0)
Chứng tỏ rằng với a và b là các số bất kì thì :
a) \(a^2+b^2-2ab\ge0\)
b) \(\dfrac{a^2+b^2}{2}\ge ab\)
\(Chứng minh các bất đẳng thức: a) (a + b)2 ≤ 2(a2 + b2) b) (a + b + c)2 ≤ 3(a2 + b2 + c2)\)
a)Ta có:
\(\left(a+b\right)^2+\left(a-b\right)^2=2\left(a^2+b^2\right)\)
Do \(\left(a-b\right)^2\ge0\),nên\(\left(a+b\right)^2\le2\left(a^2+b^2\right)\)
b)Xét \(\left(a+b+c\right)^2+\left(a-b\right)^2+\left(a-c\right)^2+\left(b-c\right)^2\)
Khai triển và rút gọn ta được:\(3\left(a^2+b^2+c^2\right)\)
Vậy \(\left(a+b+c\right)^2\le3\left(a^2+b^2+c^2\right)\)
Đúng 0
Bình luận (0)
Bài 2: (2,0 điểm)
a) Giải bất phương trình sau: 4x – 2 > 5x + 1
b) Chứng minh rằng a2 + b2 + c2 > ab + bc + ca với mọi số thực a,b,c
a) `4x-2>5x+1`
`<=>-x>3`
`<=>x<-3`
b) Theo BĐT Cauchy:
`a^2+b^2 >= 2ab`
Tương tự:
`b^2+c^2>=2bc`
`c^2+a^2>=2ca`
Cộng vế với vế: `2(a^2+b^2+c^2) >= 2(ab+bc+ca)`
`<=>a^2+b^2+c^2 >= ab+bc+ca` (ĐPCM)
Đúng 2
Bình luận (0)
a, \(4x-2>5x+1\Leftrightarrow-x>3\Leftrightarrow x< -3\)
b, Ta có : \(a^2+b^2+c^2\ge ab+bc+ca\)
\(2a^2+2b^2+2c^2\ge2ab+2bc+2ca\)
\(\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)\ge0\)
\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)* luôn đúng *
Đúng 2
Bình luận (0)





























