Rút gọn phân số:
\(\dfrac{16.29-30}{16.37+32}\)
rút gọn phân số
\(y=\frac{16.29-32}{16.37+32}\)
\(y=\frac{16.29-32}{16.37+32}=\frac{9}{13}\)
vậy y = \(\frac{9}{13}\)
t i ck nha!! 6546576876876976
Rút gọn:
\(\frac{16.29-32}{16.37+32}\)
\(\frac{16.29-32}{16.37+32}\)
\(=\frac{16.29-16.2}{16.37+16.2}\)
\(=\frac{16\left(29-2\right)}{16\left(37+2\right)}\)
\(=\frac{16.27}{16.39}\)
\(=\frac{27}{39}=\frac{9}{13}\)
Rút gọn:
\(16*29-32\over16.37+32\)
\(\frac{16.29-32}{16.37+32}\)
Rút gọn các phân số sau :
32.24
8.32
b. 84.45
49.54
c,36.10.21
23.63.35
d,16.29-32
16.37+32
a) \(\frac{3^2.2^4}{8.3^2}=\frac{3^2.2^4}{2^3.3^2}=2\)
b)\(\frac{84.45}{49.54}=\frac{2^2.7.3^3.5}{7^2.2.3^3}=\frac{10}{7}\)
c) \(\frac{36.10.21}{2^3.63.35}=\frac{2^3.3^3.5.7}{2^3.3^2.5.7^2}=\frac{3}{7}\)
d) \(\frac{16.29-32}{16.37+32}=\frac{16.29-16.2}{16.37+2.16}=\frac{16.\left(29-2\right)}{16.\left(37+2\right)}=\frac{27}{39}=\frac{9}{13}\)
Rút gọn:
\(16.29-32\over16.37+32\)
trong các phân số sau: \(\dfrac{1}{3}\), \(\dfrac{4}{7}\), \(\dfrac{8}{12}\), \(\dfrac{30}{36}\), \(\dfrac{72}{73}\)
a. Phân số nào là tối giản? vì sao?
b. Phân số nào rút gọn được. Hãy rút gọn phân số đó
a: Các phân số tối giản là \(\dfrac{1}{3};\dfrac{4}{7};\dfrac{72}{73}\) vì ƯCLN(1;3)=1; ƯCLN(4;7)=1; ƯCLN(72;73)=1
b:
Các phân số rút gọn được là
\(\dfrac{8}{12}=\dfrac{8:4}{12:4}=\dfrac{2}{3}\)
\(\dfrac{30}{36}=\dfrac{30:6}{36:6}=\dfrac{5}{6}\)
Rút gọn phân số: \(\dfrac{-270}{450}\);\(\dfrac{11}{-143}\);\(\dfrac{32}{12}\);\(\dfrac{-26}{-156}\)
\(\dfrac{-270}{450}=\dfrac{-9}{15}\)
\(\dfrac{11}{-143}=\dfrac{1}{-13}\)
\(\dfrac{32}{12}=\dfrac{8}{3}\)
\(\dfrac{-26}{-156}=\dfrac{1}{6}\)
a)Rút gọn phân số : \(\dfrac{25^{28}+25^{24}+25^{20}+.....+25^4+1}{25^{30}+25^{28}+....+25^2+1}\)
b) Cho S = 1-3 + 32-33+.....+398-399
a) Ta có: \(\dfrac{25^{28}+25^{24}+25^{20}+...+25^4+1}{25^{30}+25^{28}+...+25^2+1}\)
\(=\dfrac{25^{24}\left(25^4+1\right)+25^{16}\left(25^4+1\right)+...+\left(25^4+1\right)}{25^{28}\left(25^2+1\right)+25^{24}\left(25^2+1\right)+...+\left(25^2+1\right)}\)
\(=\dfrac{\left(25^4+1\right)\left(25^{24}+25^{16}+25^8+1\right)}{\left(25^2+1\right)\left(25^{28}+25^{24}+...+1\right)}\)
\(=\dfrac{\left(25^4+1\right)\cdot\left[25^{16}\left(25^8+1\right)+\left(25^8+1\right)\right]}{\left(25^2+1\right)\left[25^{24}\left(25^4+1\right)+25^{16}\left(25^4+1\right)+25^8\left(25^4+1\right)+\left(25^4+1\right)\right]}\)
\(=\dfrac{\left(25^4+1\right)\left(25^8+1\right)\left(25^{16}+1\right)}{\left(25^2+1\right)\left(25^4+1\right)\left(25^{24}+25^{16}+25^8+1\right)}\)
\(=\dfrac{\left(25^8+1\right)\left(25^{16}+1\right)}{\left(25^2+1\right)\left[25^{16}\left(25^8+1\right)+\left(25^8+1\right)\right]}\)
\(=\dfrac{\left(25^8+1\right)\left(25^{16}+1\right)}{\left(25^2+1\right)\left(25^8+1\right)\left(25^{16}+1\right)}\)
\(=\dfrac{1}{25^2+1}=\dfrac{1}{626}\)
a) Quan sát cách tính của Hiếu và Thảo khi rút gọn phân số \(\dfrac{12}{18}\) rồi nêu nhận xét:
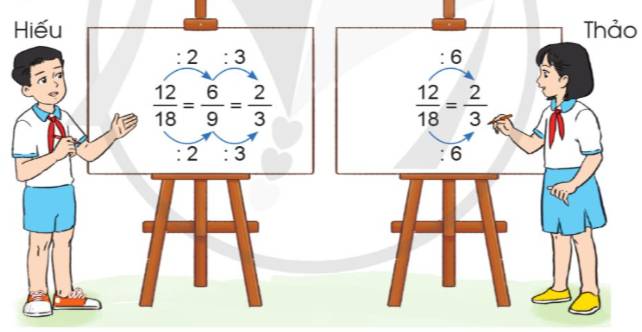
b) Rút gọn phân số \(\dfrac{30}{60}\) về dạng phân số tối giản sử dụng cách làm của Hiếu hoặc của Thảo.
a) Cách rút gọn của Thảo nhanh hơn còn của Hiếu thì lâu hơn vì phải làm nhiều bước
b) Sử dụng cách của Hiếu:
\(\dfrac{30}{60}=\dfrac{30:10}{60:10}=\dfrac{3}{6}=\dfrac{3:3}{6:3}=\dfrac{1}{2}\)
Sử dụng cách của Thảo:
\(\dfrac{30}{60}=\dfrac{30:30}{60:30}=\dfrac{1}{2}\)