Cho hình chóp SABCD đáy ABCD là hình vuông cạnh a. SA vuông góc với mp ABCD; SA = a√2. M và N là hình chiếu của A lên SB và SD.
a) CMR : AM vuông góc với SC
b) CMR : SC vuông góc (AMN)
c) Tính S tam giác SAB; SAD.
Những câu hỏi liên quan
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a tâm O,SA vuông (ABCD) và SA=a√6 a)tính khoảng cách từ A đến mp (SBC) b) tính góc giữa đường thẳng SC và mp (ABCD)
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a ,SA vuông góc với đáy và SA = a √3 /3. Góc giữa( SBC) và( ABCD) bằng bao nhiêu
\(\left\{{}\begin{matrix}BC\perp SA\subset\left(SAB\right)\\BC\perp AB\subset\left(SAB\right)\end{matrix}\right.\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)
\(\left\{{}\begin{matrix}BC\perp SB\\BC\perp AB\\\left(SBC\right)\cap\left(ABCD\right)=BC\end{matrix}\right.\Rightarrow\left(\left(SBC\right),\left(ABCD\right)\right)=\widehat{SBA}\)
\(\tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{3.a}=\dfrac{\sqrt{3}}{3}\Rightarrow\widehat{SBA}=30^0\)
Đúng 1
Bình luận (0)
Cho hình chóp SABCD có ABCD là hình vuông cạnh a, SA vuông góc với mp (ABCD) SC tạo với mp (ABCD) một góc 45 độ. Gọi E là trung điểm BC. Tính thể tích khối chóp SABCD và khoảng cách giữa hai đường thẳng DE và SC
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, SA a. Thể tích V của khối chóp SBCD là A.
V
a
3
3
B.
V
a
3
6
C.
V
a
3
4
D.
V
a...
Đọc tiếp
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, SA = a. Thể tích V của khối chóp SBCD là
A. V = a 3 3
B. V = a 3 6
C. V = a 3 4
D. V = a 3 8
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, SA a. Thể tích V của khối chóp SBCD là.
Đọc tiếp
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, SA = a. Thể tích V của khối chóp SBCD là.
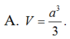
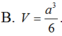
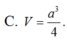
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với (ABCD) và SA = 2a. 1. Chứng minh (SCD) vuông góc với (SAD) 2. Tính d(A, (SCD))
1: CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
=>(SCD) vuông góc (SAD)
Đúng 1
Bình luận (0)
Cho hình chóp Sabcd có sa vuông góc với abcd , đáy abcd là hình chữ nhật có cạnh ab=a, ad=2a , sa= 2a căn 3
Gọi I là trung điểm của ab , mặt phẳng P qua I và vuông góc với Sb . Tính góc giữa mặt phẳng Sb và mp abcd
Giups mìnhhh với các bạn ơii , mk cần lời giải chi tiết , cảm ơnn nhiềuuu ah
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a,
S
A
a
3
và vuông góc với đáy. Góc giữa đường thẳng SD và mặt phẳng
A
B
C
D
bằng A.
60
°
B.
45
°
C.
30
°
D.
arcsin
3
5
Đọc tiếp
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, S A = a 3 và vuông góc với đáy. Góc giữa đường thẳng SD và mặt phẳng A B C D bằng
A. 60 °
B. 45 °
C. 30 °
D. arcsin 3 5
Đáp án A.
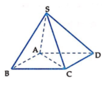
Ta có S A ⊥ ( A B C D ) nên A là hình chiếu của S trên mặt phẳng A B C D . Suy ra AD là hình chiếu của SD trên mặt phẳng A B C D .
Khi đó S D , A B C D ^ = S D , A D ^ = S D A ^ (do S D A ^ < 90 ° ).
Do Δ S A D vuông tại A nên tan S D A ^ = S A A D = a 3 a = 3 ⇒ S D A ^ = 60 ° .
Vậy S D , A B C D ^ = 60 ° .
Đúng 0
Bình luận (0)
27 tháng 4 2021 lúc 19:30
Cho hình chóp SABCD đáy là hình vuông tâm O cạnh a. SA=a căn 3. SA vuông góc với đáy. Tính góc a)(SBD) và (ABCD) b)(SBD) và (SAB) c)(SBC) và (ABCD) d)(SCD) và (ABCD)
Cho hình chóp SABCD đáy là hình vuông cạnh A, SA vuông góc với (ABCD), SA=a căn 3 a, Cm BC vuông góc với (SAB) b, Tính (SB, (ABCD)) Giúp em vơia ạ em cầm gấp
a: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
b: (SB;(ABCD))=(BS;BA)=góc SBA
\(\sin SBA=\dfrac{SA}{SB}=\dfrac{a\sqrt{3}}{2a}=\dfrac{\sqrt{3}}{2}\)
=>góc SBA=60 độ
Đúng 1
Bình luận (0)