Cho \(\widehat{xOy}\) & \(\widehat{yOz}\) là 2 góc kề bù. \(Ot\) là tia phân giác của \(\widehat{xOy}\). Trong \(\widehat{yOz}\) vẽ \(Om\) \(\perp\) \(Ot\). Chứng minh rằng: \(Om\) là tia phân giác của \(\widehat{yOz}\)

Những câu hỏi liên quan
Cho \(\widehat{xOy}\)\(=100^o\),vẽ tia \(Oz\) trong \(\widehat{xOy}\) sao cho \(\widehat{xOz}\)\(=40^o\).Tính \(\widehat{zOy}\).
Cho \(\widehat{xOy}\)\(=100^o\) vẽ tia \(Oz\) trong \(\widehat{xOy}\) sao cho \(\widehat{xOz}\) \(=40^o\),Tính \(\widehat{zOy}\).
Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOz}< \widehat{xOy}\left(40^0< 100^0\right)\)
nên tia Oz nằm giữa hai tia Ox và Oy
\(\Leftrightarrow\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)
\(\Leftrightarrow\widehat{yOz}+40^0=100^0\)
hay \(\widehat{yOz}=60^0\)
Vậy: \(\widehat{yOz}=60^0\)
Đúng 1
Bình luận (0)
Cho hai góc \(\widehat {xOy},\widehat {yOz}\) kề bù với nhau. Biết \(\widehat {xOy} = 25^\circ \). Tính \(\widehat {yOz}\).
Vì hai góc \(\widehat {xOy},\widehat {yOz}\) kề bù với nhau nên
\(\begin{array}{l}\widehat {xOy} + \widehat {yOz} = 180^\circ \\ \Rightarrow 25^\circ + \widehat {yOz} = 180^\circ \\ \Rightarrow \widehat {yOz} = 180^\circ - 25^\circ = 155^\circ \end{array}\)
Đúng 0
Bình luận (0)
Bài 2: Cho góc tù \(\widehat{xOy}\). Vẽ \(\widehat{xOt}\) và \(\widehat{yOz}\) là 2 góc kề bù với \(\widehat{xOy}\). Chứng minh \(\widehat{xOt}\) và \(\widehat{yOz}\) đối đỉnh.
xOy + tOx = 180o ( kề bù)
xOy + yOz = 180o ( kề bù)
mà xOy = xOy.
=> 2 góc này bằng nhau ( 2 góc cùng kề bù với góc thứ 3 thì bằng nhau).
=> 2 góc đối đỉnh.
like và tim bạn nhé
Đúng 1
Bình luận (1)
2 góc cùng kề bù với 1 góc thì = nhau vì:
vd: góc thứ 3 = 80o thì 2 kề bù với góc 80o sẽ = 100o
nghe giống người thứ 3 nhưng không phải nha.![]()
Đúng 0
Bình luận (0)
a) Quan sát Hình 1 và cho biết hai góc widehat {xOy} và widehat {yOz} có:- Cạnh nào chung?- Điểm trong nào chung?b) Hãy đo các góc widehat {xOy},widehat {yOz},widehat {xOz} trong Hình 1 rồi so sánh tổng số đo của widehat {xOy} và widehat {yOz} với widehat {xOz}.c) Tính tổng số đo của hai góc widehat {mOn} và widehat {nOp} trong Hình 2.
Đọc tiếp
a) Quan sát Hình 1 và cho biết hai góc \(\widehat {xOy}\) và \(\widehat {yOz}\) có:
- Cạnh nào chung?
- Điểm trong nào chung?
b) Hãy đo các góc \(\widehat {xOy},\widehat {yOz},\widehat {xOz}\) trong Hình 1 rồi so sánh tổng số đo của \(\widehat {xOy}\) và \(\widehat {yOz}\) với \(\widehat {xOz}\).
c) Tính tổng số đo của hai góc \(\widehat {mOn}\) và \(\widehat {nOp}\) trong Hình 2.
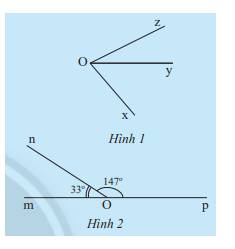
a) Hai góc \(\widehat {xOy}\) và \(\widehat {yOz}\) có cạnh Oy chung, không có điểm trong chung
b) Ta có:
\(\begin{array}{l}\widehat {xOy} = 30^\circ ,\widehat {yOz} = 45^\circ ,\widehat {xOz} = 75^\circ \\ \Rightarrow \widehat {xOy} + \widehat {yOz} = \widehat {xOz}\end{array}\)
c) Ta có: \(\widehat {mOn} + \widehat {nOp} = 33^\circ + 147^\circ = 180^\circ \)
Đúng 0
Bình luận (0)
Quan sát Hình 14.
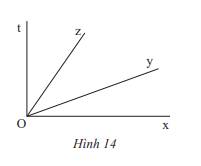
a) Tìm các góc kề với \(\widehat {xOy}\).
b) Tìm số đo của \(\widehat {tOz}\) nếu cho biết \(\widehat {xOy} = 20^\circ ;\widehat {xOt} = 90^\circ ;\widehat {yOz} = \widehat {tOz}\).
a) Các góc kề với \(\widehat {xOy}\) là: \(\widehat {yOz};\widehat {yOt}\)
b) Ta có:
\(\begin{array}{l}\widehat {xOy} + \widehat {yOz} + \widehat {zOt} = \widehat {xOt}\\ \Rightarrow 20^\circ + \widehat {zOt} + \widehat {zOt} = 90^\circ \\ \Rightarrow 2.\widehat {zOt} = 90^\circ - 20^\circ = 70^\circ \\ \Rightarrow \widehat {zOt} = 70^\circ :2 = 35^\circ \end{array}\)
Đúng 0
Bình luận (0)
Cho góc $\widehat{xOy}$ và tia $Oz$ nằm trong góc đó sao cho $\widehat{xOz}=4 \cdot \widehat{yOz}$. Tia phân giác $Ot$ của góc $\widehat{xOz}$ thỏa mãn $Ot \perp Oy$.
Tính số đo của góc $\widehat{xOy}$.
`Answer:`
Ta có `hat{zOt}+\hat{yOz}=90^o`
\(\Rightarrow\frac{1}{2}.Oz+\widehat{yOz}=90^o\)
\(\Rightarrow\frac{1}{2}.4\widehat{yOz}+\widehat{yOz}=90^o\)
\(\Rightarrow\widehat{yOz}.3=90^o\)
\(\Rightarrow\widehat{yOz}=30^o\)
`=>\hat{xOz}=120^o` (Vì `\hat{xOz}=4\hat{yOz}`
Vậy `\hat{xOy}=\hat{yOz}+\hat{xOz}=120^o+30^o=150^o`
Xem thêm câu trả lời
Cho 3 góc kề nhau widehat{xOy,},widehat{yOz,}widehat{zOt}.Có tổng số đo bằng 180 độBiết widehat{xoy}2.widehat{yoz},widehat{yoz}3widehat{zot}(Vẽ hình)a) Tinh widehat{xOy,}widehat{yOz,}widehat{zOt}B)Vẽ tia phân giác Om và On của widehat{xOy},widehat{yOz.}Tínhwidehat{mOn}
Đọc tiếp
Cho 3 góc kề nhau \(\widehat{xOy,}\),\(\widehat{yOz,}\)\(\widehat{zOt}\).Có tổng số đo bằng 180 độ
Biết \(\widehat{xoy}=2.\widehat{yoz},\widehat{yoz}=3\widehat{zot}\)(Vẽ hình)
a) Tinh \(\widehat{xOy,}\widehat{yOz,}\widehat{zOt}\)
B)Vẽ tia phân giác Om và On của \(\widehat{xOy},\widehat{yOz.}\)Tính\(\widehat{mOn}\)
true or false 1, If Ox and Oy are opposite rays then widehat{xOy180^o}2,If Ox and Oy are parallel then widehat{xOy}180^o or widehat{xOy}0^o3, If widehat{xOy}90^o then widehat{xOy} is a straight angle4, If widehat{xOy} +widehat{yOz}180^o then widehat{xOy} and widehat{yOz} are complementary5, If widehat{xOy} is larger than widehat{xOz} then widehat{xOz} is an acute angle6, the lagest angle which is form by two rays is an obtuse angle7, Two acute angles cannot be supplementary8,widehat{xOy} and wi...
Đọc tiếp
true or false
1, If Ox and Oy are opposite rays then \(\widehat{xOy=180^o}\)
2,If Ox and Oy are parallel then \(\widehat{xOy}=180^o\) or \(\widehat{xOy}=0^o\)
3, If \(\widehat{xOy}=90^o\) then \(\widehat{xOy}\) is a straight angle
4, If \(\widehat{xOy}\) +\(\widehat{yOz}=180^o\) then \(\widehat{xOy}\) and \(\widehat{yOz}\) are complementary
5, If \(\widehat{xOy}\) is larger than \(\widehat{xOz}\) then \(\widehat{xOz}\) is an acute angle
6, the lagest angle which is form by two rays is an obtuse angle
7, Two acute angles cannot be supplementary
8,\(\widehat{xOy}\) and \(\widehat{yOz}\) are adjacent
9, if \(\widehat{xOy}\) and \(\widehat{zOy}\)are supplementary then one of them must be an obtuse angle
10,if \(\widehat{xOy}\) and \(\widehat{yOz}\) are adjacent then \(\widehat{xOy}\) > \(\widehat{xOz}\)
11, If Ox lies between Oy and Oz then \(\widehat{xOy}\) and \(\widehat{yOz}\) are adjacent
1: T
2: F
3: F
4: T
5: F
6: F
7: T
8: T
9: F
10: F
11: F
Đúng 0
Bình luận (0)
Cho \(\widehat{xOy}\). Tia Oz nằm trong \(\widehat{xOy}\)sao cho \(\widehat{xOz}\)=4. \(\widehat{yOz}\).Tia phân giác Ot của \(\widehat{xOz}\)vuông góc với tia Oy. Tính \(\widehat{xOy}\)
vì ot vuông góc với oy => góc xot =90 độ
mà ot là tia phân giác của góc xoy => góc xoy=2.xot =180 độ
vì góc xoz nằm trong góc xoy và góc xoz =4.yoz
=> yoz+4yoz=180 độ
=> 5yoz = 180 độ
=> yoz=36
=> xoz=36.4=144
p/s: đề bảo tính một mk xoy nhưng họ cho cả xoz, yoz mk nghĩ pk có liên quan nên tính thêm :>
Đúng 0
Bình luận (0)
Xin lỗi bạn Tiểu Hy_Queen, nhưng bạn đã làm sai rồi. Đáp án :\(\widehat{xOy}\)=150 độ
Đúng 0
Bình luận (0)





















