a: Xét (O) có

PE,PM là tiếp tuyến

=>PE=PM và IP là phân giác của góc EIM(1)

Xét (O) có
QE,QN là tiếp tuyến

=>QE=QN và IQ là phân giác của góc EIN(2)

PQ=PE+EQ

=>PQ=PM+QN

b: Từ (1), (2) suy ra góc PIQ=1/2*180=90 độ

c: Gọi O là trung điểm của PQ

Xét hình thang MNQP có

O,I lần lượt là trung điểm của PQ,MN

=>OI là đường trung bình

=>OI vuông góc MN

=>MN là tiếp tuyến của (O)

trời ơi rối quá , ai biết làm thì làm đi 

a) Xét tứ giác BFEC: ^BFC=^BEC=90⁰ => Tứ giác BFEC là tứ giác nội tiếp đường tròn (đpcm).

b) Dễ thấy tứ giác ABKC nội tiếp đường tròn (O) => ^CAK=^CBK hay ^CAN=^CBK (1)

AK là đường kính của (O); B nằm trên (O) => AB\(\perp\)BK

Mà CF\(\perp\)AB => BK//CF => ^CBK=^BCF (2)

(1); (2) => ^CAN=^BCF. Mà ^BCF=^CAH (Cùng phụ ^ABC) => ^CAN=^BAH hay ^CAN=^FAM

Lại có: ^ACN=^AHE (Cùng phụ ^HAC) 

Dễ chứng minh tứ giác AFHE nội tiếp đường tròn => ^AHE=^AFE

=> ^ACN=^AFE. Hay ^ACN=^AFM

Xét \(\Delta\)AMF và \(\Delta\)ANC: ^ACN=^AFM; ^CAN=^FAM => \(\Delta\)AMF ~ \(\Delta\)ANC (g.g)

=> \(\frac{AM}{AN}=\frac{MF}{NC}\)(*)

=> ^AMF=^ANC => 180⁰ - ^AMF=180⁰ - ^ANC => ^FMH=^CNK

Tứ giác ABKC nội tiếp (O) => ^ABC=^AKC. Mà ^ABC=^AHF (Cùng phụ ^BAH)

=> ^AKC=^AHF hay ^NKC=^MHF.

Xét \(\Delta\)NCK và \(\Delta\)MFH: ^NKC=^MHF; ^CNK=^FMH => \(\Delta\)NKC ~ \(\Delta\)MFH (g.g)

=> \(\frac{HM}{NK}=\frac{FM}{NC}\)(**)

Từ (*) và (**) => \(\frac{AM}{AN}=\frac{HM}{NK}\Rightarrow\frac{AM}{HM}=\frac{AN}{NK}\)=> MN//HK (Định lí Thales đảo) (đpcm).

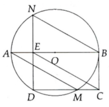
a, HS tự chứng minh

b, Ta chứng minh được tứ giác BCEN là hình bình hành => BC = EN

Do BCDE là hình bình hành

=> BC = ED; DE = EN

=> BA ⊥ EN => BABC

=> BC là tiếp tuyến

a.

Ta có \(MA=MB\) (t/c hai tiếp tuyến cắt nhau)

\(OA=OB=R\)

\(\Rightarrow OM\) là trung trực AB hay OM vuông góc AB

AC là đường kính và B là điểm thuộc đường tròn \(\Rightarrow\widehat{ABC}\) là góc nội tiếp chắn nửa đường tròn

\(\Rightarrow\widehat{ABC}=90^0\Rightarrow AB\perp BC\)

\(\Rightarrow BC||OM\) (cùng vuông góc AB)

b.

Do MA là tiếp tuyến \(\Rightarrow AM\perp AC\) hay tam giác MAC vuông tại A

AC là đường kính và K thuộc đường tròn \(\Rightarrow\widehat{AKC}\) là góc nt chắn nửa đường tròn

\(\Rightarrow\widehat{AKC}=90^0\) hay AK là đường cao trong tam giác vuông MAC

Áp dụng hệ thức lượng:

\(AC^2=CK.CM\Rightarrow CK.CM=\left(2R\right)^2=4R^2\)

c.

Em có nhầm đề ko nhỉ, vì 2 góc này hiển nhiên bằng nhau, ko cần chứng minh, do 1 góc là góc nội tiếp và 1 góc là góc tạo bởi tiếp tuyến và dây cung, cùng chắn cung BK.

a, Xét tam giác ADB và tam giác AEC , ta có 

góc EDC = góc ACE = 90 độ ( góc ACE là góc nội tiếp chắn nửa đường tròn )

góc ABD = góc AEC  ( 2 góc nội tiếp cùng chắn cung AC )

\(\Leftrightarrow\)tam giác ADB đồng dạng với tam giác AEC (g_g)

\(\Rightarrow\)\(\frac{AD}{AB}=\frac{AC}{AE}\)( Các cặp góc tương ứng )

hay AD.AE=AB.AC