Xét ΔABC vuông tại A, có đường cao AH:

\(BC^2=AB^2+AC^2\left(pytago\right)\\ \Leftrightarrow BC^2=3^2+4^2\\ \Leftrightarrow BC^2=25\\ \Leftrightarrow BC=5cm\\ AB^2=BH.BC\\ \Leftrightarrow3^2=BH.5\\ \Leftrightarrow9=BH.5\\ \Leftrightarrow BH=1,8cm\)

giải cả HA nhe

a: AC=8cm

b: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)

c: AH=4,8cm

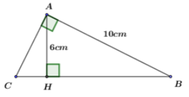
Áp dụng định lý Pytago trong tam giác ABH vuông tại H. Ta có:

Trong tam giác vuông ABC vuông tại A có AH là đường cao

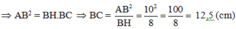
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:

Vậy AC = 7,5 (cm); BC =  12,5 (cm)

Đáp án cần chọn là: B

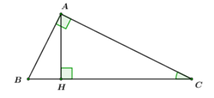
Áp dụng định lý Pytago trong ∆ ABC vuông tại A ta có:

Áp dụng hệ thức lượng trong  ∆ ABC vuông tại A có đường cao AH ta có:

Đáp án cần chọn là: B

Tính được AH =  50 17 cm; S A B C = 15 c m 2

Xét \(\Delta AHC\left(\widehat{AHC}=90^o\right)\) có:

\(AC^2=AH^2+HC^2\) (định lí pitago)

\(\Rightarrow AH^2=AC^2-HC^2\)

\(\Rightarrow AH=\sqrt{5^2-4^2}=3\left(cm\right)\)

Xét \(\Delta ABC\left(\widehat{BAC}=90^o\right)\) có:

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\) (hệ thức lượng trong tam giác vuông)

\(\Rightarrow\dfrac{1}{AB^2}=\dfrac{1}{AH^2}-\dfrac{1}{AC^2}\)

\(\Rightarrow\dfrac{1}{AB^2}=\dfrac{1}{3^2}-\dfrac{1}{5^2}\)

\(\Rightarrow AB=3,75\left(cm\right)\)

Xét \(\Delta ABC\left(\widehat{BAC}=90^o\right)\) có:

\(BC^2=AB^2+AC^2\) (định lí pitago)

\(\Rightarrow BC=\sqrt{3,75^2+5^2}=6,25\left(cm\right)\)

\(AH=\sqrt{AC^2-HC^2}=3\left(cm\right)\)

\(HB=\dfrac{AH^2}{HC}=\dfrac{3^2}{4}=2.25\left(cm\right)\)

BC=HB+HC=4+2,25=6,25(cm)

\(AB=\sqrt{6.25^2-5^2}=3.75\left(cm\right)\)

dễ vcl