cho hình bình hành ABCD có AB=a , BC=b, BD=m ,AC=n . chứng minh rằng:
m2 +n2 =2 (a2+b2)
Những câu hỏi liên quan
Cho hình bình hành ABCD có AB = a, BC = b, BD = m, AC = n. Chứng minh rằng: m2 + n2 = 2(a2 + b2).
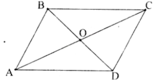
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
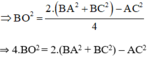
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có AB = a; BC = b; BD = m và AC = n.
Chứng minh rằng : \(m^2+n^2=2\left(a^2+b^2\right)\) ?
Áp dụng định lí về đường trung tuyến:
OA2 = -
(1)
Thay OA = , AB = a, AD = BC = b và BD = m vào (1) ta có:
\(\left(\dfrac{n}{2}\right)^2=\dfrac{b^2+a^2}{2}-\dfrac{m^2}{4}\)
\(\Leftrightarrow\dfrac{n^2}{4}+\dfrac{m^2}{4}=\dfrac{a^2+b^2}{2}\)
\(\Leftrightarrow m^2+n^2=2\left(a^2+b^2\right)\)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có AB=2BC. Gọi M và N là Trung điểm của AB, CD. a) chứng minh rằng AMND là hình thoi. b)chứng minh rằng MBND là hình bình hành. C) chứng minh rằng AC, BD, MN đồng quy
Cho hình bình ABCD có AB = a, BC = b, BD = m và AC = n. Chứng minh rằng m bình phương + n bình phương = 2( a bình phương + b bình phương)
Gọi giao điểm của AC và BD là O
Ta có: \(OB^2=\dfrac{2\left(AB^2+BC^2\right)-AC^2}{4}\)
\(\Leftrightarrow\) \(4OB^2+AC^2=2\left(AB^2+BC^2\right)\)
\(\Leftrightarrow\) \(BD^2+AC^2=2\left(AB^2+BC^2\right)\) (Do \(4OB^2=\left(2OB\right)^2\) mà 2OB = BD)
\(\Leftrightarrow\) \(m^2+n^2=2\left(a^2+b^2\right)\) (đpcm)
Chúc bn học tốt!
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD có AB = a, BC = b ,BD = m, và AC = n. Chứng minh rằng m2 + n2 = 2(a2 + b2 )
Áp dụng định lí về đường trung tuyến:
OA2 = –
Thay OA = , AB = a
AD = BC = b và BD = m => dpcm
Đúng 1
Bình luận (0)
cho hình bình hành ABCD có AB=a, AD=b
chứng minh rằng AC2+BD2=2(a2+b2)
- Gọi E là giao điểm của AC và BD
△ABE có trung tuyến BE
\(\Rightarrow BE^2=\dfrac{2\left(AB^2+BC^2\right)-AC^2}{4}\)
\(\Rightarrow4.BE^2=2\left(AB^2+BC^2\right)-AC^2\)
Mà O là trung điểm BD \(\Rightarrow BD=2.BE\Rightarrow BD^2=4.BE^2\)
\(\Rightarrow BD^2=2\left(AB^2+BC^2\right)-AC^2\)
\(\Rightarrow BD^2+AC^2=2\left(AB^2+BC^2\right)\)
Vậy: \(AC^2+BD^2=2\left(a^2+b^2\right)\left(đpcm\right)\)
(Hình như đây là Toán 10?)
Đúng 1
Bình luận (0)
Lời giải:
Kẻ đường cao $BH, DT$ của hình bình hành
Dễ chứng minh $\triangle ADT =\triangle BCH$ (ch-gn)
$\Rightarrow DT=CH; AT=BH$
Áp dụng định lý Pitago:
$AC^2+BD^2=AT^2+TC^2+BH^2+DH^2$
$=(AT^2+BH^2)+TC^2+DH^2)$
$=2AT^2+(DC-DT)^2+(DC+CH)^2$
$=2(AD^2-DT^2)+(DC-DT)^2+(DC-DT)^2$
$=2(b^2-DT^2)+(a-DT)^2+(a+DT)^2$
$=2(b^2+a^2)$
Ta có đpcm.
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có AB=2BC. Gọi M và N là Trung điểm của AB, CD.
a) chứng minh rằng AMND là hình thoi.
b)chứng minh rằng MBND là hình bình hành.
C) chứng minh rằng AC, BD, MN đồng quy
Cho hình bình hành ABCD có BC = AC. Gọi I là trung điểm cạnh CD, M là giao của BD và AI;
N là giao của AB và CM. Chứng minh rằng CN = BD
Cho hình bình hành ABCD (AB > BC) có M, N lần lượt là trung điểm của AB vàCD. a) Tứ giác AMCN là hình gì? Vì sao? b) Chứng minh: AC, BD, MN đồng quy
Cho hình bình hành ABCD, tia phân giác góc B cắt CD tại M, tia phân giác góc D cắt AB tại N
a) chứng minh rằng BMDN là hình bình hành
b)chứng minh rằng AC, BD, MN đồng quy
(Tự vẽ hình nhen)
a,Ta có ABCD là hbh => gADC=gABC(1)
BM là phân giác gABC(gt)=>gABM=1/2gABC(2)
DN là phân giác gADC(gt)=>gMDN=1/2gADC(3)
Từ(1),(2) và (3)=> gNDM=gNBM
Mặt khác NB//DM(t/c hbh)=> BMDN là hbh
b,Gọi O là giao điểm của AC và BD(4)
=>O là trung điểm của BD(t/c hbh)
Ta lại có BMDN là hbh(câu a)=>O cũng là trung điểm của MN(5)
Từ (4) và (5)=>AC,BD,MN đồng quy tại O
Đúng 0
Bình luận (0)