Bài 2: 

a: Ta có: ΔABC cân tại A

mà AH là đường cao

nên AH là tia phân giác của góc BAC

b: Xét ΔAMH vuông tại M và ΔANH vuông tại N có

AH chung

\(\widehat{MAH}=\widehat{NAH}\)

Do đó: ΔAMH=ΔANH

Suy ra: AM=AN

hay ΔAMN cân tại A

c: Xét ΔABC có AM/AB=AN/AC

nên MN//BC

d: \(AH^2-AN^2=HN^2\)

\(BH^2-BM^2=MH^2\)

mà HN=MH

nên \(AH^2-AN^2=BH^2-BM^2\)

hay \(AH^2+BM^2=BH^2+AN^2\)

Câu 2.

a) Cho 2 khí lội qua dung dịch AgNO3/NH3

+Khí nào phản ứng có kết tủa : propin

 CH≡C–CH3 + AgNO3 + NH3 → AgC≡C–CH3 + NH4NO3

+Khí còn lại không có hiện tượng : propen

b) Trích mỗi chất 1 ít làm mẫu thử

- Cho dung dịch Cu(OH)2 vào từng mẫu thử

+ Mẫu thử nào phản ứng, xuất hiện dung dịch màu xanh lam là Glyxerol

Cu(OH)2 + 2C3H5(OH)3 ⟶ 2H2O + [C3H5(OH)2O]2Cu

+ 2 mẫu thử còn lại không phản ứng là ancol etylic và phenol 

- Cho dung dịch Brom vào 2 mẫu thử không phản ứng với Cu(OH)2

+ Mẫu thử nào xuất hiện kết tủa : C6H5OH

3Br2 + C6H5OH ⟶ C6H2Br3OH + 3HBr

+ Còn lại không phản ứng là C2H5OH

Câu 1

1. CH3-CH=CH2 + HBr ---------> CH3-CH2-CH2Br

CH3-CH=CH2 + HBr ---------> CH3-CHBr-CH3

2.CH≡CH + 2 AgNO3 + 2 NH3 ---------> AgC≡CAg↓ + 2 NH4NO3

3.C2H5OH + Na ----------> C2H5ONa + \(\dfrac{1}{2}\)H2

4. \(2CH_{\text{4}}-^{1500^oC,lln}\rightarrow C_2H_2+2H_2\)

5. CH₃CH(OH)CH2CH3  \(-^{170^oC,H_2SO_4}\rightarrow\) CH3CH=CHCH3  + H2O

 CH3CH(OH)CH2CH3  \(-^{170^oC,H_2SO_4}\rightarrow\)  CH3CH2CH=CH2  +H2O

6. C6H5OH + NaOH ------> C6H5ONa + H2O

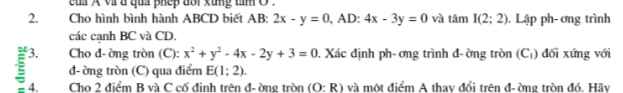
Do A đối xứng C qua I, B đối xứng D qua I

\(\Rightarrow\) CD đối xứng AB qua I và BC đối xứng AD qua I

Hay CD là ảnh của AB qua phép đối xứng tâm I, BC là ảnh của AD qua phép đối xứng tâm I

Gọi \(M\left(x;y\right)\) là 1 điểm thuộc AB \(\Rightarrow2x-y=0\) (1)

M' là ảnh của M qua phép đối xứng tâm I \(\Rightarrow M'\in DC\)

\(\left\{{}\begin{matrix}x'=2.2-x\\y=2.2-y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4-x'\\y=4-y'\end{matrix}\right.\) thế vào (1):

\(2\left(4-x'\right)-\left(4-y'\right)=0\Leftrightarrow-2x'+y'+4=0\Leftrightarrow2x'-y'-4=0\)

Hay pt CD có dạng: \(2x-y-4=0\)

Tương tự gọi \(N\left(x;y\right)\in AD\Rightarrow4x-3y=0\) (2)

N' là ảnh của N qua phép đối xứng tâm I

\(\Rightarrow\left\{{}\begin{matrix}x'=4-x\\y'=4-y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4-x'\\y=4-y'\end{matrix}\right.\) thế vào (2):

\(4\left(4-x'\right)-3\left(4-y'\right)=0\) \(\Leftrightarrow-4x'+3y'+4=0\Leftrightarrow4x'-3y'-4=0\)

Hay pt BC: \(4x-3y-4=0\)

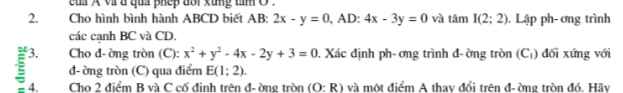
Đường tròn (C) có pt:

\(\left(x-2\right)^2+\left(y-1\right)^2=2\Rightarrow\) (C) tâm \(I\left(2;1\right)\) bán kính \(R=\sqrt{2}\)

\(\left(C_1\right)\) đối xứng (C) qua E \(\Rightarrow\left(C_1\right)\) có tâm \(I_1\) là ảnh của I qua phép đối xứng tâm I và bán kính \(R_1=R=\sqrt{2}\)

\(\left\{{}\begin{matrix}x_{I_1}=2x_E-x_I=0\\y_{I1}=2y_E-y_I=3\end{matrix}\right.\)

Phương trình: \(x^2+\left(y-3\right)^2=2\)

1 If my father didn't smoke too much, he wouldn'e have a bad cold

2 If she were tall enough, she could join the basketball team

3 If I had much time, I would visit my grandparents very often

4 If he knew her address, he could visit her

5 If the bike weren't too small, I could ride it

6 If they had enough money, they would buy the tickets for the concerts

7 If I had a car, I wouldn't have to get up early to catch the bus

8 If Mark were't talkative, people would like him 

9 If Ken played football well enough, he would be chosen to be in the school team

10 If Emma read book often, her essays wouldn't be bad

nói c₁ với c₂ ta có đoạn o₁o₂

-vẽ đường trung trục của o₁o₂ .và đườn đó là MN như hình vẽ

-phép đôí xứng trục qua MN sẽ biến (c₁) thành (c₂).như vậy ta có đc đpcm

16:

a: ĐKXĐ: x>0

\(x+\dfrac{1}{x}+\sqrt{x}+\dfrac{1}{\sqrt{x}}=4\)

\(x+\dfrac{1}{x}>=2\cdot\sqrt{x\cdot\dfrac{1}{x}}=2\)

\(\sqrt{x}+\dfrac{1}{\sqrt{x}}>=2\cdot\sqrt{\sqrt{x}\cdot\dfrac{1}{\sqrt{x}}}=2\)

Do đó: \(x+\dfrac{1}{x}+\sqrt{x}+\dfrac{1}{\sqrt{x}}>=2+2=4\)

Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x^2=1\\x=1\end{matrix}\right.\)

=>x=1