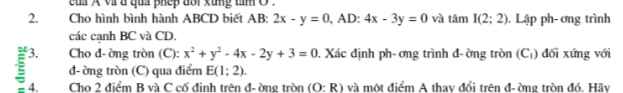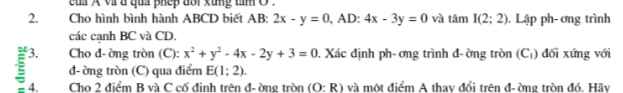Do A đối xứng C qua I, B đối xứng D qua I
\(\Rightarrow\) CD đối xứng AB qua I và BC đối xứng AD qua I
Hay CD là ảnh của AB qua phép đối xứng tâm I, BC là ảnh của AD qua phép đối xứng tâm I
Gọi \(M\left(x;y\right)\) là 1 điểm thuộc AB \(\Rightarrow2x-y=0\) (1)
M' là ảnh của M qua phép đối xứng tâm I \(\Rightarrow M'\in DC\)
\(\left\{{}\begin{matrix}x'=2.2-x\\y=2.2-y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4-x'\\y=4-y'\end{matrix}\right.\) thế vào (1):
\(2\left(4-x'\right)-\left(4-y'\right)=0\Leftrightarrow-2x'+y'+4=0\Leftrightarrow2x'-y'-4=0\)
Hay pt CD có dạng: \(2x-y-4=0\)
Tương tự gọi \(N\left(x;y\right)\in AD\Rightarrow4x-3y=0\) (2)
N' là ảnh của N qua phép đối xứng tâm I
\(\Rightarrow\left\{{}\begin{matrix}x'=4-x\\y'=4-y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4-x'\\y=4-y'\end{matrix}\right.\) thế vào (2):
\(4\left(4-x'\right)-3\left(4-y'\right)=0\) \(\Leftrightarrow-4x'+3y'+4=0\Leftrightarrow4x'-3y'-4=0\)
Hay pt BC: \(4x-3y-4=0\)