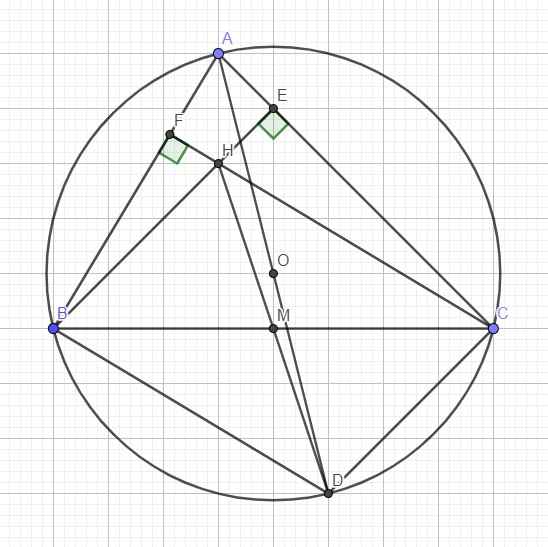
Gọi M là trung điểm BC, nối AO kéo dài cắt (O) tại D
Kẻ các đường cao BE, CF cắt nhau tại H
Ta có: \(\widehat{ABD}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow BD\perp AB\)
Lại có \(CF\perp AB\) (giả thiết)
\(\Rightarrow BD||CF\)
Hoàn toàn tương tự, ta có \(CD||BE\)
\(\Rightarrow\) Tứ giác BHCD là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow\) Hai đường chéo BC và HD cắt nhau tại trung điểm các đường
Hay M cũng là trung điểm HD
Hay H đối xứng D qua M cố định
Mà tập hợp D là đường tròn (O) cố định
\(\Rightarrow\) Tập hợp H là ảnh của (O) qua phép đối xứng tâm M cố định
Vậy trực tâm của tam giác ABC nằm trên đường tròn cố định là ảnh của (O) qua phép đối xứng tâm M