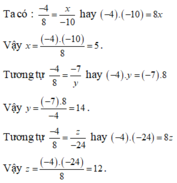\(x\) + y = 2;  ⇒ y = 2 - \(x\); 

y + z  = 3   ⇒ y  = 3 - z 

⇒ 2 - \(x\) = 3 - z ⇒ \(x\) = 2 - 3 + z ⇒ \(x\) = -1 + z

Thay \(x\) = -1 + z vào biểu thức z + \(x\) = -5 ta có:

z  - 1 + z = -5

2z = -5 + 1 ⇒ 2z = -4 ⇒ z = -4: 2 ⇒ z = -2

Thay z = -2 vào biểu thức \(x\) = -1 + z ta có \(x\) = -1 -2 = -3

Thay  z = -2 vào biểu thức y = 3 - z ta có: y  = 3 - (-2) = 5

Thanks

Bài 1

a) (x + 3)(x + 2) = 0

x + 3 = 0 hoặc x + 2 = 0

*) x + 3 = 0

x = 0 - 3

x = -3 (nhận)

*) x + 2 = 0

x = 0 - 2

x = -2 (nhận)

Vậy x = -3; x = -2

b) (7 - x)³ = -8

(7 - x)³ = (-2)³

7 - x = -2

x = 7 + 2

x = 9 (nhận)

Vậy x = 9

Bài 3

20a + 10b = 2010

10b = 2010 - 20a

b = (2010 - 20a) : 10

*) a = 0

b = (2010 - 20.0) : 10 = 201

*) a = 1

b = (2010 - 10.1) : 10 = 200

*) a = 2

b = (2010 - 10.2) : 10 = 199

Vậy ta có ba cặp số nguyên (a; b) thỏa mãn:

(0; 201); (1; 200); (2; 199)

Xét \(x\le y\le z\) vì x,y,z nguyên dương

\(\Rightarrow xyz\ne0\)và \(x\le y\le z\Rightarrow xyz=x+y+z\le3z\)

\(\Rightarrow xy\le3\Rightarrow xy\in\left\{1;2;3\right\}\)

- Nếu \(xy=1\Rightarrow x=y=1\)ta có: \(2+z=z\)( không thỏa mãn )

- Nếu \(xy=2\Rightarrow x=1;y=2\Rightarrow z=3\)( thỏa mãn ) ( vì \(x\le y\))

- Nếu \(xy=3\Rightarrow x=1;y=3\Rightarrow z=2\)( thỏa mãn ) ( vì \(x\le y\))

Vậy......................................

 \(\text{Do vai trò bình đẳng của x, y, z trong phương trình, trước hết ta xét x ≤ y ≤ z. }\)
Vì \(x,y,z\)nguyên dương nên xyz ≠ 0, do x ≤ y ≤ z => xyz = x + y + z ≤ 3z => xy ≤ 3 
=> xy thuộc {1 ; 2 ; 3}. 
Nếu xy = 1 => x = y = 1, thay vào (2) ta có : 2 + z = z, vô lí. 
Nếu xy = 2, do x ≤ y nên x = 1 và y = 2, thay vào (2), => z = 3. 
Nếu xy = 3, do x ≤ y nên x = 1 và y = 3, thay vào (2), => z = 2. 
Vậy nghiệm nguyên dương của phương trình (2) là các hoán vị của (1 ; 2 ; 3).

Ta có: \(x+y+z=xyz\)

\(\Leftrightarrow\left(x\cdot100\right)+\left(y\cdot10\right)+\left(z\cdot1\right)=xyz\)

\(\Rightarrow z=0,1,2,3,4,5,6,7,8,9\)

\(\Rightarrow y=0,1,2,3,4,5,6,7,8,9\)

\(\Rightarrow x=1,2,3,4,5,6,7,8,9\)

bạn ơi bây giờ bạn đã có cách làm bài trên chưa?

Chỉ giúp mình với

Cảm ơn nhiều ạ

<=> \(x^3-x+y^{3_{ }}-y+z^3-z=2017\)

<=>\(\left(x-1\right)x\left(x+1\right)+\left(y-1\right)y\left(y+1\right)+\left(z-1\right)z\left(z+1\right)=2017\)(1)

vì \(x-1;x;x+1\)là 3 sô nguyên liên tiếp nên tích của chúng chia hết cho 3=>vế trái (1) chia hết cho 3

Mà 2017 không chia hết cho 3

=>Phương trình đã cho vô nghiệm

\(\frac{x}{2}=\frac{8}{y}=\frac{-12}{z}=2\)

1. \(\frac{x}{2}=\frac{2}{1}\)Mà \(\frac{2}{1}=\frac{4}{2}\)\(\Rightarrow x=4\)

Ta có :\(\frac{4}{2}=\frac{8}{y}\)\(\Leftrightarrow\frac{8}{4}=\frac{8}{y}\)\(\Rightarrow y=4\)

Ta lại có : \(\frac{-12}{z}=\frac{2}{1}\)\(\Leftrightarrow\frac{-12}{z}=\frac{-12}{-6}\)\(\Rightarrow z=-6\)

K/l : Vậy \(x=4;y=4;z=-6\)

ta có /x-2/ >= 0 với mọi x

/x+y/>=0

/y+z/>= 0

  nên để      /x-2/+/x+y/+/y+z/=0 thì

*/x-2/=0

=>x-2=0

=>x=2

*/x+y/=0

=>x+y=0

=>x=y (1)

*/y+z/=0

=>y+z=0 

=>y=z (2)

từ (1) và (2) suy ra x=y=z mà x=2 =>y=z=2

Vậy x=y=z=2

phần đàu sai phải là \(\ge\)0 

nhưng chưa tìm được dấu đó nên đành dùng tạm