 Help me bài 2 , 3 . Thanks nhiều nhiều ạ
Help me bài 2 , 3 . Thanks nhiều nhiều ạ

Những câu hỏi liên quan
Help me bài 2 vs mọi ng`
@Hoàng Thị Ngọc Anh, @Nguyễn Huy Tú, ... và mọi người. Thanks nhiều ạ.

a)Ta có: AC<AB
=>\(\widehat{ADC}\)<\(\widehat{ADB}\)
b)
Đúng 0
Bình luận (1)
Cho 2 đa thức : f(x) = -2x2 - 3x3 - 5x + 5x3 - x + x2 + 4x + 3 + 4x2
g(x) = 2x2 - x3 + 3x + 3x3 + x2 - x - 9x + 2
a) Tìm h(x) = f(x) - g(x)
b) Tìm nghiệm của đa thức h(x)
HELP ME!!!THANKS CÁC CẬU NHIỀU LẮM Ạ!!
h(x)=5x+1
nghiệm_của_đa_thức_h(x)_là_-1/5
Đúng 0
Bình luận (0)
Cho 2 đa thức : f(x) = -2x2 - 3x3 - 5x + 5x3 - x + x2 + 4x + 3 + 4x2
g(x) = 2x2 - x3 + 3x + 3x3 + x2 - x - 9x + 2
a) Tìm h(x) = f(x) - g(x)
b) Tìm nghiệm của đa thức h(x)
HELP ME!!!THANKS CÁC CẬU NHIỀU LẮM Ạ!!
a)h(x)=f(x)-g(x)
=(2x3 +3x2 -2x +3)-(2x3 +3x2 -7x +2)
=2x3 + 3x2 - 2x +3 - 2x3 -3x2 + 7x -2
=5x+1
b)h(x)=5x+1=0
=>5x=-1
x=\(\frac{-1}{5}\)
Đúng 0
Bình luận (0)
Cho A = \(3+3^2+3^3+...+3^{2008}\)
Tìm x biết 2A + 3 = 3x
Mai mk thi r . HELP ME !!!! Thanks các bạn nhiều
Ta có :\(A=3+3^2+3^3+...+3^{2008}\)(1)
\(\Rightarrow3A=3^2+3^3+3^4+...+3^{2009}\)(2)
Lấy (2) trừ đi 1 ta có :
\(\Rightarrow2A=3^{2009}-3\)
Ta lại có :
\(2A+3=3^x\)
\(\Rightarrow3^{2009}=3^x\)
\(\Rightarrow x=2009\)
Đúng 0
Bình luận (0)
/ 2x - 3 / = 3 - 2x
Các bạn ơi giải giúp mik bài này vs ạ! Đáp án của bài này là S = {x ∈ R / x =< 3/2} mà mik ko biết cách giải ạ! Ai biết giúp mik vs! Thanks nhiều!
\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)
Đúng 1
Bình luận (0)
Cho 2 đa thức : f(x) = -2x2 - 3x3 - 5x + 5x3 - x + x2 + 4x + 3 + 4x2
g(x) = 2x2 - x3 + 3x + 3x3 + x2 - x - 9x + 2
a) Tìm h(x) = f(x) - g(x)
b) Tìm nghiệm của đa thức h(x)
HELP ME!!!THANKS CÁC CẬU NHIỀU LẮM Ạ!!
a) Tìm h(x) = f(x) - g(x)
f(x) - g(x) = (-2x2 - 3x3 - 5x + 5x3 - x + x2 + 4x + 3 + 4x2) - (2x2 - x3 + 3x + 3x3 + x2 - x - 9x + 2)
= -2x2 - 3x3 - 5x + 5x3 - x + x2 + 4x + 3 + 4x2 - 2x2 + x3 - 3x - 3x3 - x2 + x + 9x - 2
= (-2x2 + x2 + 4x2 - 2x2 - x2) + (-3x3 + 5x3 + x3 - 3x3) + (-5x - x + 4x - 3x + x + 9x) + (3 - 2)
= 5x + 1
Vậy h(x) = 5x + 1
b) Tìm nghiệm của đa thức h(x)
Cho h(x) = 0
\(\Leftrightarrow\) 5x + 1 = 0
5x = 0 + 1
5x = 1
x = \(\dfrac{1}{5}\)
Vậy x = \(\dfrac{1}{5}\) là nghiệm của đa thức h(x).
Đúng 0
Bình luận (0)
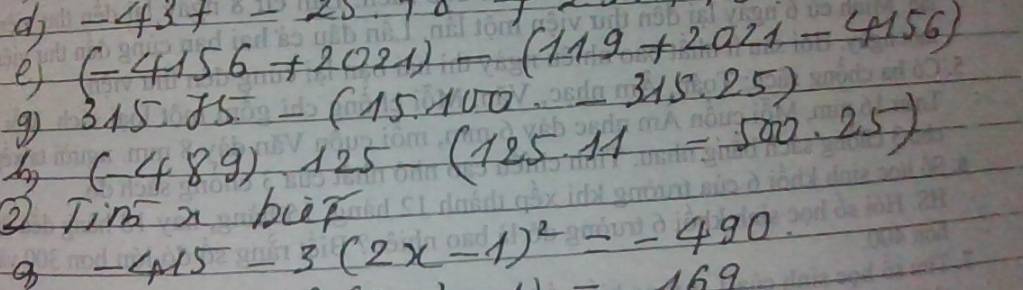
cần giúp gấp từ phần e bên trên + vs phần a bài tìm x ạ, thanks nhiều <3
e: \(\left(-4156+2021\right)-\left(119+2021-4156\right)\)
\(=-4156+2021-119-2021+4156\)
\(=\left(-4156+4156\right)+\left(2021-2021\right)-119\)
=0+0-119
=-119
g: \(315\cdot75-\left(15\cdot100-315\cdot25\right)\)
\(=315\cdot75-15\cdot100+315\cdot25\)
\(=315\left(75+25\right)-15\cdot100\)
\(=315\cdot100-15\cdot100=300\cdot100=30000\)
h: \(\left(-489\right)\cdot125-\left(125\cdot11-500\cdot25\right)\)
\(=-489\cdot125-125\cdot11+500\cdot25\)
\(=125\left(-489-11\right)+500\cdot25\)
\(=125\cdot\left(-500\right)+500\cdot25\)
\(=500\left(-125+25\right)\)
\(=500\cdot\left(-100\right)=-50000\)
Bài 2:
a: \(-415-3\left(2x-1\right)^2=-490\)
=>\(3\left(2x-1\right)^2+415=490\)
=>\(3\left(2x-1\right)^2=75\)
=>\(\left(2x-1\right)^2=25\)
=>\(\left[{}\begin{matrix}2x-1=5\\2x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=-4\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Có ai đang buồn và lo lắng như này ko?
Help làm bài này: S = (1 + 2/3) . (1 + 2/5) . (1 + 2/7) ..... (1 + 2/89)
Thanks nhiều nha.
Tôi đây
Ko biết làm bt đó
# USAS - 12 #
Đúng 0
Bình luận (0)
\(=\frac{5}{3}.\frac{7}{5}.\frac{9}{7}......\frac{91}{89}\)
\(=\frac{91}{3}\)
@@@@@@@@@@@2
Đúng 0
Bình luận (0)
\(S=\left(1+\frac{2}{3}\right).\left(1+\frac{2}{5}\right)....\left(1+\frac{2}{89}\right)\)
\(\Rightarrow S=\frac{5}{3}.\frac{7}{5}....\frac{91}{89}\)
\(\Rightarrow S=\frac{5.7.9.....89.91}{3.5.7.....87.89}\)
\(\Rightarrow S=\frac{91}{3}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho A = \(3+3^2+3^3+...+3^{2008}\)
Tìm x biết 2A + 3 = 3x
Mai mk thi r . HELP ME !!!! Thanks các bạn nhiều
Ta có: \(A=3+3^2+3^3+...+3^{2008}\)
\(\Rightarrow3A=3^2+3^3+3^4+...+3^{2009}\)
Trừ \(3A-A=3^2+3^3+3^4+...+3^{2009}-3-3^2-3^3-...-3^{2008}\)
\(\Rightarrow2A=3^{2009}-3\)
Mà \(2A=3^x-3\)
\(\Rightarrow3^x=3^{2009}\)
\(\Rightarrow x=2009.\)
Vậy x = 2009.
Đúng 0
Bình luận (0)
\(a=3+3^2+3^3+...+3^{2008}\)
\(3a=3^2+3^3+3^4+...+3^{2009}\)
\(3a-a=\left(3^2+3^3+3^4+...+3^{2009}\right)-\left(3+3^2+3^3+...+3^{2008}\right)\)
\(2a=3^{2009}-3\)
\(2a+3=3^{2009}=3^x\)
\(x=2009\)
Đúng 0
Bình luận (0)
\(A=3+3^2+3^3+......+3^{2008}\)
\(\Leftrightarrow3A=3^2+3^3+......+3^{2009}\)
\(\Leftrightarrow3A-A=\left(3^2+3^3+3^4......+3^{2009}\right)-\left(3+3^2+3^3+......+3^{2008}\right)\)
\(\Leftrightarrow2A=3^{2009}-3\)
\(\Leftrightarrow2A+3=3^{2009}=3^x\)
Vậy \(x=2009\) để \(2A+3=3^x\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời

























