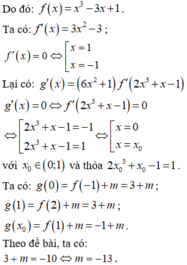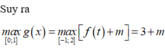Tìm x, z, y, q, m, r, t trên hình vẽ biết QP//NO

Những câu hỏi liên quan
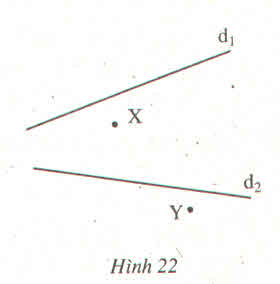
Vẽ hình 22 vào vở rồi tìm điểm Z trên đường thẳng d1 và điểm T trên đường thẳng d2 sao cho X, Z, T thẳng hàng và Y, Z, T thẳng hàng.
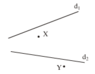
Hình 22
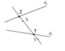
Vì X, Z, T thẳng hàng và Y, Z, T thẳng hàng nên cả 4 điểm này đều nằm trên đường thẳng XY.
Cách vẽ: Vẽ đường thẳng XY cắt d1 tại Z, cắt d2 tại T.
Đúng 0
Bình luận (0)
Hãy tìm tất cả các h/s f(x) x/đ ; liên tục trên R ; lấy giá trị trong R và t/m các đ/k : \(f\left(x-y\right)f\left(y-z\right)f\left(z-x\right)+8=0\) \(\forall x;y;z\in R\)
Vẽ hình 22 vào vở rồi tìm điểm Z trên đường thẳng \(d_1\) và điểm T trên đường thẳng \(d_2\) sao cho X, Z, T thẳng hàng và Y, Z, T thẳng hàng ?
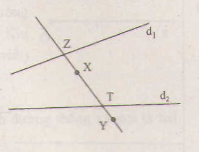
- Ba điểm X,Z,T thẳng hàng vậy X nằm trên đường thẳng ZT.
- Ba điểm Y,Z,T thẳng hàng vì vậy Y nằm trên đường thẳng ZT.
Suy ra X,Y nằm trên đường thẳng ZT, dó đó 4 điểm Z,Y,Z,T thẳng hàng.
Các vẽ: vẽ đường thẳng XY cắt đường thẳng d1 tài Z , cắt đường thẳng d2 tại T
Đúng 0
Bình luận (0)
Vẽ hình 22 vào vở rồi tìm điểm Z trên đường thẳng d1 và điểm T trên đường thẳng d2 sao cho X, Z, T thẳng hàng và Y, Z, T thẳng hàng
 Ba điểm X,Z,T thẳng hàng vậy X nằm trên đường thẳng ZT.
Ba điểm X,Z,T thẳng hàng vậy X nằm trên đường thẳng ZT.
- Ba điểm Y,Z,T thẳng hàng vì vậy Y nằm trên đường thẳng ZT.
Suy ra X,Y nằm trên đường thẳng ZT, dó đó 4 điểm Z,Y,Z,T thẳng hàng.
Các vẽ: vẽ đường thẳng XY cắt đường thẳng d1 tài Z , cắt đường thẳng d2 tại T
Đúng 0
Bình luận (0)
Giải:

- Ba điểm X,Z,T thẳng hàng vậy X nằm trên đường thẳng ZT.
- Ba điểm Y,Z,T thẳng hàng vì vậy Y nằm trên đường thẳng ZT.
Suy ra X,Y nằm trên đường thẳng ZT, dó đó 4 điểm Z,Y,Z,T thẳng hàng.
Các vẽ: vẽ đường thẳng XY cắt đường thẳng d1 tài Z , cắt đường thẳng d2 tại T
Đúng 0
Bình luận (0)
Cho hàm số yf(x) liên tục và có đạo hàm trên R. Biết hàm số f’(x) có đồ thị được cho trong hình vẽ. Tìm điều kiện của m để hàm số g(x)f(2019)x – mx +2 đồng biến trên [0;1]
Đọc tiếp
Cho hàm số y=f(x) liên tục và có đạo hàm trên R. Biết hàm số f’(x) có đồ thị được cho trong hình vẽ. Tìm điều kiện của m để hàm số g(x)=f(2019)x – mx +2 đồng biến trên [0;1]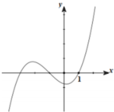
![]()
![]()
![]()
![]()
Tìm tích của xyz biết x,y và z \(\in\) R+ để \(x\left(y+z\right)=32\) ; \(y\left(x+z\right)=27\) ; \(z\left(x+y\right)=35\)
\(x\left(y+z\right)=32;y\left(x+z\right)=27;z\left(x+y\right)=35\\ \Rightarrow\left(xy+xz\right)+\left(xy+yz\right)+\left(xz+yz\right)=32+27+35\\ \Rightarrow2\left(xy+yz+zx\right)=94\\ \Rightarrow xy+yz+xz=47\\ \Rightarrow yz=15;xz=20;xy=12\\ \Rightarrow\left(x.y.z\right)^2=3600\)
Ta có : x;y;z khác 0 nên x.y.z khác 0
=> x.y.z=60
Đúng 0
Bình luận (0)
tìm x,y,z biết \(\frac{x+y+1}{2}\)=\(\frac{y+z+1}{1}\)=\(\frac{x+z-2}{y}\)=x+y+z
help mai nộp rùi ae ơi
đề đâu ra mà khó thế
tớ chịu
tìm x,y,z biết ràng
\(\frac{2x}{5}=\frac{3y}{10}=\frac{z}{12}\) và x+y+z=109
Lời giải:
Đặt $\frac{2x}{5}=\frac{3y}{10}=\frac{z}{12}=t$
$\Rightarrow x=\frac{5}{2}t; y=\frac{10}{3}t; z=12t$
Khi đó:
$x+y+z=109$
$\Leftrightarrow \frac{5}{2}t+\frac{10}{3}t+12t=109$
$\Leftrightarrow \frac{107}{6}t=109\Rightarrow t=\frac{654}{107}$
$\Rightarrow x=\frac{5}{2}t=\frac{1635}{107}; y=\frac{10}{3}t=\frac{2180}{107}; z=12t=\frac{7848}{107}$
Đúng 0
Bình luận (0)
Cho hàm số
y
f
x
có đạo hàm trên R và có đồ thị như hình vẽ. Đặt hàm số
y
g
x
f
2
x
3
+
x
-
1
+
m
.
Tìm m để
m
a
x...
Đọc tiếp
Cho hàm số y = f x có đạo hàm trên R và có đồ thị như hình vẽ. Đặt hàm số y = g x = f 2 x 3 + x - 1 + m . Tìm m để m a x 0 ; 1 g = - 10
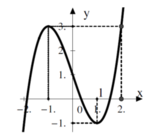
A. m = -1
B. m = 3
C. m = -12
D. m = -13