Giải theo cách này mà giải chi tiết hơn được ko ạ. Đang cần gấp!!!
Cảm ơn ạ!!!

Những câu hỏi liên quan
Toán lớp 7 này e ko bt lm ạ,mà e đang cần,ai giúp e giải chi tiết dễ hiểu đc ko ạ,e cảm ơn nhiều lắm ạ!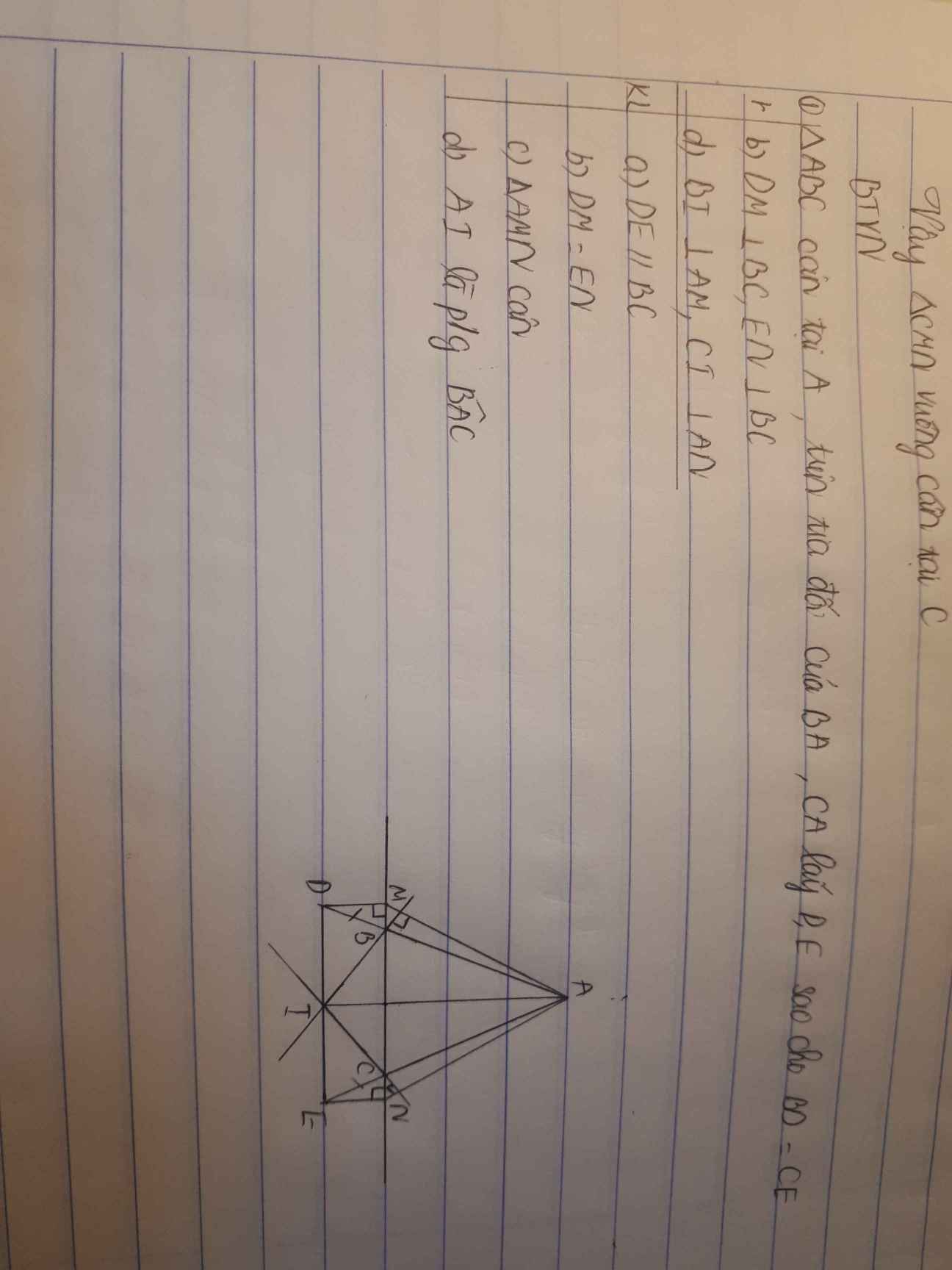
Mình chưa hiểu bài này lắm. Có thể giải chi tiết dùm được hông ạ.
Đang cần gấp
Cảm ơn trc nha
Đề bài: Trục căn thức ở mẫu và rút gọn (nếu được)
Vì mình ko biết gõ ra thành chữ nên chỉ có hình,mọi người thông cảm ạ!
Mọi người giúp mình giải bài này nhé, càng chi tiết càng tốt ạ
Mình đang cần gấp
Cảm ơn mọi người đã giúp đỡ ạ
Đọc tiếp
 Đề bài: Trục căn thức ở mẫu và rút gọn (nếu được)
Đề bài: Trục căn thức ở mẫu và rút gọn (nếu được)
Vì mình ko biết gõ ra thành chữ nên chỉ có hình,mọi người thông cảm ạ!
Mọi người giúp mình giải bài này nhé, càng chi tiết càng tốt ạ
Mình đang cần gấp
Cảm ơn mọi người đã giúp đỡ ạ
2\(\sqrt{\dfrac{16}{3}}\) - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{11}{2\sqrt{3}}\)
= \(\dfrac{11\sqrt{3}}{6}\)
f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5\sqrt{2}}{4}\)
Đúng 2
Bình luận (0)
(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{3-1}\)
= \(\dfrac{-4}{2}\)
= -2
Đúng 2
Bình luận (0)
\(\dfrac{2}{\sqrt{6}-2}+\dfrac{2}{\sqrt{6}+2}+\dfrac{5}{\sqrt{6}}\)
= \(\dfrac{2.\left(\sqrt{6}+2\right)+2\left(\sqrt{6}-4\right)}{\left(\sqrt{6}-2\right)}\) + \(\dfrac{5}{\sqrt{6}}\)
= \(\dfrac{2\sqrt{6}+4+2\sqrt{6}-4}{6-4}\) + \(\dfrac{5\sqrt{6}}{6}\)
= \(\dfrac{4\sqrt{6}}{2}\) + \(\dfrac{5\sqrt{6}}{6}\)
= \(\dfrac{12\sqrt{6}+5\sqrt{6}}{6}\)
= \(\dfrac{17\sqrt{6}}{6}\)
Đúng 1
Bình luận (0)
Giải hết và chi tiết với ạ. Em đang cần gấp ạ. Em cảm ơn nhiều ạ.
Đọc tiếp




 Giải hết và chi tiết với ạ. Em đang cần gấp ạ. Em cảm ơn nhiều ạ.
Giải hết và chi tiết với ạ. Em đang cần gấp ạ. Em cảm ơn nhiều ạ.
Giải chi tiết pt 3 và 4 giúp em với ạ. Em đang cần gấp. Em cảm ơn ạ
4.
\(sinx+2cos\left(x+\dfrac{\pi}{3}\right)+4sin\left(x+\dfrac{\pi}{6}\right)+cosx=4\)
\(\Leftrightarrow sinx+cosx-\sqrt{3}sinx+2\sqrt{3}sinx+2cosx+cosx=4\)
\(\Leftrightarrow\left(1+\sqrt{3}\right)sinx+4cosx=4\)
\(\Leftrightarrow\sqrt{20+2\sqrt{3}}\left(\dfrac{1+\sqrt{3}}{\sqrt{20+2\sqrt{3}}}sinx+\dfrac{4}{\sqrt{20+2\sqrt{3}}}cosx\right)=4\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}\right)=\dfrac{4}{\sqrt{20+2\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}=\pm arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
3.
\(4sinx+cosx+2cos\left(x+\dfrac{\pi}{3}\right)=2\)
\(\Leftrightarrow4sinx+cosx+cosx-\sqrt{3}sinx=2\)
\(\Leftrightarrow\left(4-\sqrt{3}\right)sinx+2cosx=2\)
\(\Leftrightarrow\sqrt{23-4\sqrt{3}}\left(\dfrac{4-\sqrt{3}}{\sqrt{23-4\sqrt{3}}}sinx+\dfrac{2}{\sqrt{23-4\sqrt{3}}}cosx\right)=2\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}\right)=\dfrac{2}{\sqrt{23-4\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}=\pm arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
ai giải chi tiết hơn cho mình được ko vậy, mình đang cần rất gấp, rất cần lun đó nha mình cảm ơn
Đọc tiếp
ai giải chi tiết hơn cho mình được ko vậy, mình đang cần rất gấp, rất cần lun đó nha mình cảm ơn
Gọi số vở 7A,7B,7C ll là a,b,c(quyển;a,b,c∈N*)
Áp dụng tc dstbn:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+c}{2+4}=\dfrac{120}{8}=15\\ \Rightarrow\left\{{}\begin{matrix}a=30\\b=45\\c=60\end{matrix}\right.\)
Vậy ...
Đúng 1
Bình luận (0)
Câu này trên mạng đã có lời giải nhưng mà mình chẳng hiểu gì cả. Cầu cao nhân giúp đỡ ạ. Chỉ cho mình cách giải nào dễ hiểu hơn được không? Ghi chi tiết ra càng tốt. Mình vô cùng cảm ơn:,((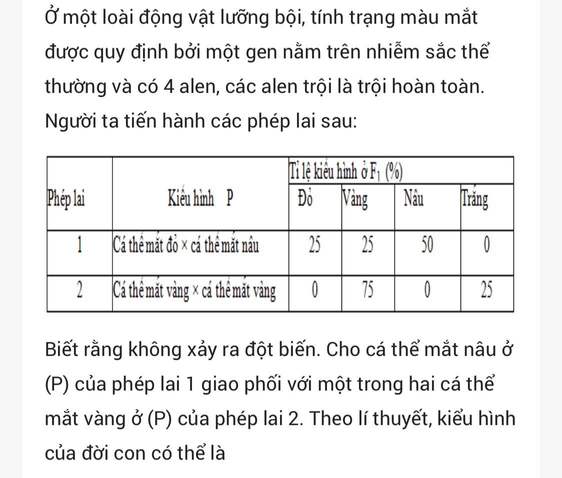
 Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ
Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ
a: Xét tứ giác AECF có
AE//CF(AB//CD)
AE=CF
Do đó: AECF là hình bình hành
b: AE+EB=AB
CF+FD=CD
mà AE=CF và AB=CD
nên BE=DF
Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
=>DE=BF
c:
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔAIC có
D,O lần lượt là trung điểm của AI,AC
=>DO là đường trung bình
=>DO//CI
d: AECF là hình bình hành
=>AC cắt EF tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của EF
=>AC,EF,BD đồng quy(do cùng đi qua O)
Đúng 0
Bình luận (0)
Huhu các cao nhân giúp mình với mình đang cần gấp, mình cảm ơn ạ. Nếu được câu giải chi tiết cho mình với :((((((.
a: Xét ΔSBM và ΔSNB có
\(\widehat{SBM}=\widehat{SNB}\)
\(\widehat{BSM}\) chung
Do đó: ΔSBM\(\sim\)ΔSNB
Suy ra: SB/SN=SM/SB
hay \(SB^2=SM\cdot SN\)
b: Xét (O) có
SA là tiếp tuyến
SB là tiếp tuyến
Do đó: SA=SB
mà OA=OB
nên SO là đường trung trực của AB
=>SO⊥AB
Xét ΔOBS vuông tại B có BH là đường cao
nên \(SH\cdot SO=SB^2=SM\cdot SN\)
Đúng 1
Bình luận (0)















