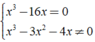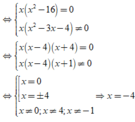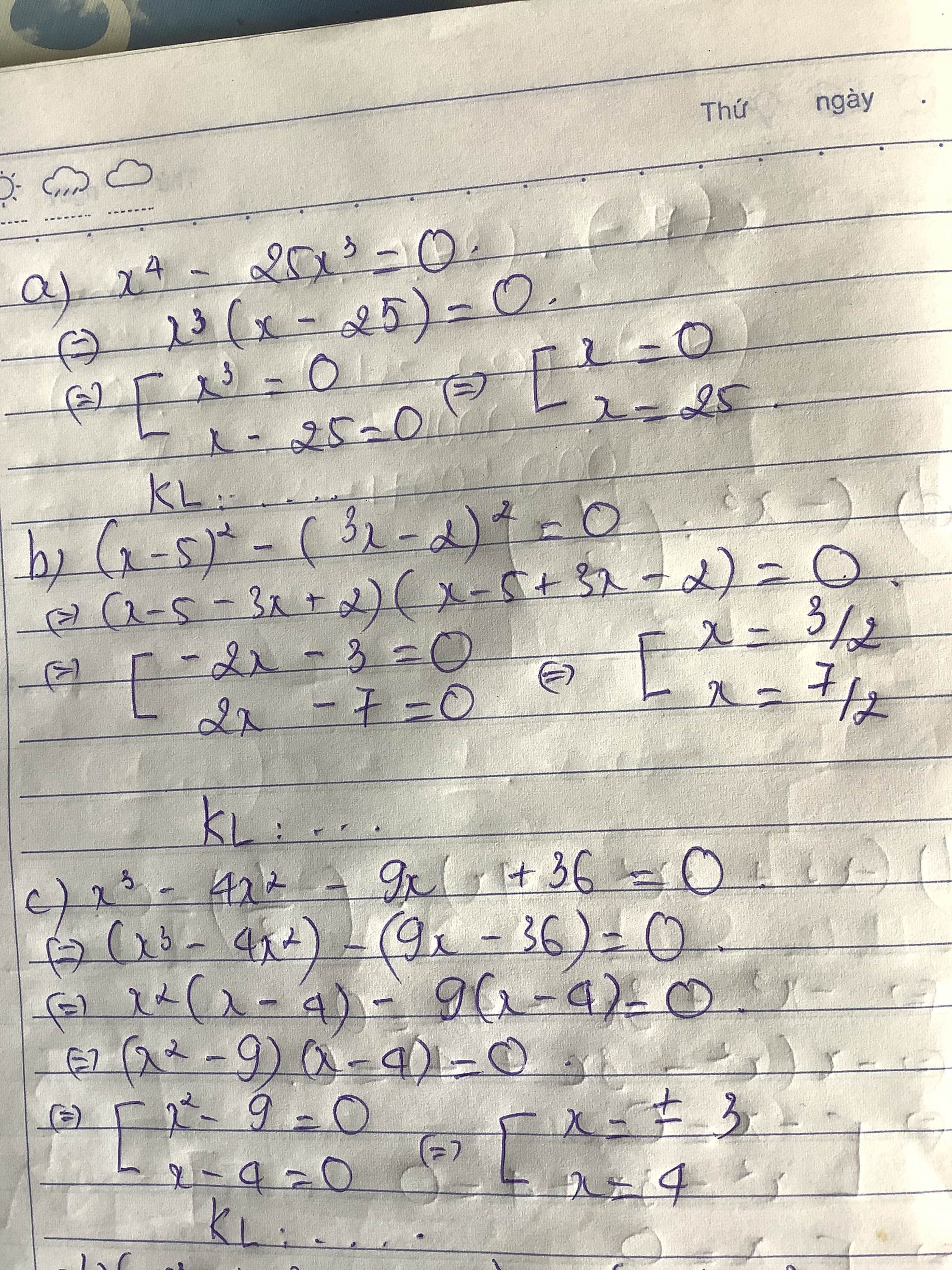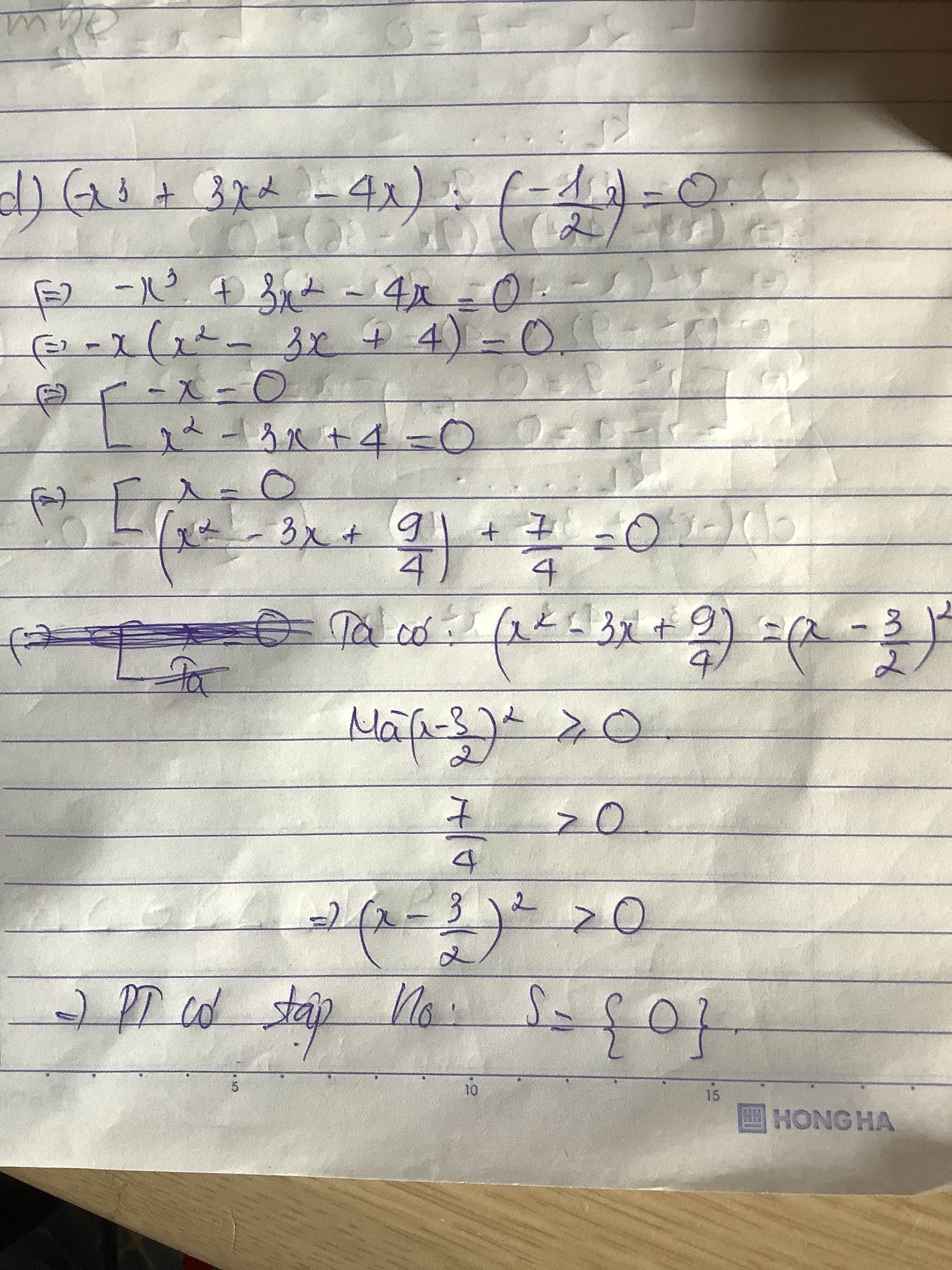x3-3x2-4x+12=0

Những câu hỏi liên quan
Gọi
z
1
,
z
2
là hai nghiệm phức của phương trình
x
3
−
3
x
2
+
4
x
−
12
0.
Tính giá trị biểu thức
P
z
1
−
z
2
.
A. 4...
Đọc tiếp
Gọi z 1 , z 2 là hai nghiệm phức của phương trình x 3 − 3 x 2 + 4 x − 12 = 0. Tính giá trị biểu thức P = z 1 − z 2 .
A. 4
B. 8
C. 2
D. 0
Đáp án D
x 3 − 3 x 2 + 4 x − 12 = 0 ⇔ x 2 x − 3 + 4 x − 3 = 0 ⇔ x − 3 x 2 + 4 = 0 ⇔ x = 2 i x = − 2 i x = 3 .
Vậy z 1 − z 2 = 0.
Đúng 0
Bình luận (0)
x3-3x2-4x+12
Nếu đề bài là phân tích đa thức thành nhân tử thì làm như sau:
\(x^3-3x^2-4x+12\)
\(=x ^2\left(x-3\right)-4\left(x-3\right)\)
\(=\left(x-3\right)\left(x^2-4\right)\)
\(=\left(x-3\right)\left(x^2+2x-2x-4\right)\)
\(=\left(x-3\right)\left[x\left(x+2\right)-2\left(x+2\right)\right]\)
\(=\left(x-3\right)\left(x+2\right)\left(x-2\right)\)
Nếu đề là tìm nghiệm thì làm đến đó ta làm tiếp:
\(\Leftrightarrow\)\(x-3=0\)\(\Leftrightarrow\)\(x=3\)
hoặc \(x+2=0\)\(\Leftrightarrow\)\(x=-2\)
hoặc \(x-2=0\)\(\Leftrightarrow\)\(x=2\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử: x 3 - 3 x 2 - 4 x + 12
x 3 - 3 x 2 - 4 x + 12 = x 3 - 3 x 2 - 4 x - 12 = x 2 x - 3 - 4 x - 3 = x - 3 x 2 - 4 = x - 3 x + 2 x - 2
Đúng 0
Bình luận (0)
Tìm x:
a) x3-3x2+3x-1=1000
b) x2-4x-21=0
a.
\(\Leftrightarrow\left(x-1\right)^3=10^3\)
\(\Leftrightarrow x-1=10\)
\(\Rightarrow x=11\)
b.
\(\Leftrightarrow x^2-4x+4=25\)
\(\Leftrightarrow\left(x-2\right)^2=5^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=5\\x-2=-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-3\end{matrix}\right.\)
Đúng 0
Bình luận (0)
a) x3-3x2+3x-1=1000
⇒(x-1)3=1000
⇒x-1=10
⇒x=11
b) x2-4x-21=0
⇒ x2-7x+3x-21=0
⇒x(x-7)+3(x-7)=0
⇒(x+3)(x-7)=0
⇒ hoặc x+3 = 0 ⇒ x=-3
hoặc x-7=0⇒x=7
vậy x={-3; 7}
Đúng 0
Bình luận (0)
a) Có: \(x^3-3x^2.1+3.1^2x-1^3=1000\)
\(\Rightarrow\left(x-3\right)^3=1000\)
\(\Rightarrow\left[{}\begin{matrix}x-3=10\\x-3=-10\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=13\\x=-7\end{matrix}\right.\)
b) Có: \(x^2-4x+4-25=0\)
\(\Rightarrow\left(x-2\right)^2=25\)
\(\Rightarrow\left[{}\begin{matrix}x-2=5\\x-2=-5\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=7\\x=-3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giá trị của x để phân thức x 3 - 16 x x 3 - 3 x 2 - 4 x bằng 0
A. x = ± 4.
B. x ≠ 1.
C. x = 0.
D. x = - 1.
Giá trị của x để phân thức
x
3
-
16
x
x
3
-
3
x
2
-
4
x
bằng 0 ? A. x ± 4. B. x ≠ 1. C. x -4. D. x - 1.
Đọc tiếp
Giá trị của x để phân thức x 3 - 16 x x 3 - 3 x 2 - 4 x bằng 0 ?
A. x = ± 4.
B. x ≠ 1.
C. x = -4.
D. x = - 1.
Tìm x:
a) x4-25x3=0
b) (x-5)2-(3x-2)2=0
c) x3-4x2-9x+36=0
d) (-x3+3x2-4x) : (\(-\dfrac{1}{2}\)x)=0
a.
$x^4-25x^3=0$
$\Leftrightarrow x^3(x-25)=0$
\(\Leftrightarrow \left[\begin{matrix} x^3=0\\ x-25=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=0\\ x=25\end{matrix}\right.\)
b.
$(x-5)^2-(3x-2)^2=0$
$\Leftrightarrow (x-5-3x+2)(x-5+3x-2)=0$
$\Leftrightarrow (-2x-3)(4x-7)=0$
\(\Leftrightarrow \left[\begin{matrix}
-2x-3=0\\
4x-7=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix}
x=\frac{-3}{2}\\
x=\frac{7}{4}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
c.
$x^3-4x^2-9x+36=0$
$\Leftrightarrow x^2(x-4)-9(x-4)=0$
$\Leftrightarrow (x-4)(x^2-9)=0$
$\Leftrightarrow (x-4)(x-3)(x+3)=0$
\(\Leftrightarrow \left[\begin{matrix} x-4=0\\ x-3=0\\ x+3=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=4\\ x=3\\ x=-3\end{matrix}\right.\)
d. ĐK: $x\neq 0$
$(-x^3+3x^2-4x):(\frac{-1}{2}x)=0$
$\Leftrightarrow x(-x^2+3x-4):(\frac{-1}{2}x)=0$
$\Leftrightarrow -2(-x^2+3x-4)=0$
$\Leftrightarrow x^2-3x+4=0$
$\Leftrightarrow (x-1,5)^2=-1,75< 0$ (vô lý)
Vậy pt vô nghiệm.
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
1) Phân tích đa thức thành nhân tử
a) xy2 – 25x
b) x(x – y) + 2x – 2y
c) x3 – 3x2 – 4x + 12
\(a,=x\left(y^2-25\right)=x\left(y-5\right)\left(y+5\right)\\ b,=x\left(x-y\right)+2\left(x-y\right)=\left(x+2\right)\left(x-y\right)\\ c,=x^2\left(x-3\right)-4\left(x-3\right)\\ =\left(x-2\right)\left(x+2\right)\left(x-3\right)\)
Đúng 1
Bình luận (0)
Phân tích các đa thức sau thành nhân tử:
a) xy2-25x
b) x(x-y)2x-2y
c) x3-3x2-4x+12
a) \(xy^2-25x=x\left(y^2-25\right)=x\left(y-5\right)\left(y+5\right)\)
b) \(x\left(x-y\right)+2x-2y=x\left(x-y\right)+\left(2x-2y\right)=x\left(x-y\right)+2\left(x-y\right)=\left(x-y\right)\left(x+2\right)\)
c) \(x^3-3x^2-4x+12=\left(x^3-3x^2\right)-\left(4x-12\right)=x^2\left(x-3\right)-4\left(x-3\right)=\left(x-3\right)\left(x^2-4\right)=\left(x-2\right)\left(x-3\right)\left(x+2\right)\)
Đúng 1
Bình luận (0)
\(a,=x\left(y^2-25\right)=x\left(y-5\right)\left(y+5\right)\\ b,=x\left(x-y\right)+2\left(x-y\right)=\left(x+2\right)\left(x-y\right)\\ c,=x^2\left(x-3\right)-4\left(x-3\right)=\left(x-2\right)\left(x+2\right)\left(x-3\right)\)
Đúng 2
Bình luận (0)
\(x\left(y^2-25\right)=y\left(y-5\right)\left(y+5\right)\)
\(x\left(x-y\right)2\left(x-y\right)=\left(x-y\right)2x\)
\(x^2\left(x-3\right)-4\left(x-3\right)=\left(x^2-4\right)\left(x-3\right)=\left(x-2\right)\left(x+2\right)\left(x-3\right)\)
Đúng 1
Bình luận (0)













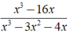
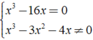
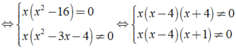
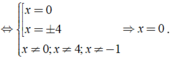
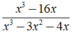 bằng 0 ⇔
bằng 0 ⇔