Chỉ giúp em mấy câu này vs
Em cảm ơn nhiều .

Những câu hỏi liên quan
Ai chỉ rm mấy câu này với .
Em cảm ơn nhiều
17. Despite promising that he wouldn't be late, he didn't arrive until 9 o'clock.
18. I didn't use to listen to Western music some years ago.
19. My mum used to be a chef in Cham restaurant, but now he is retired.
20. There used to be a market here in 2003.
21. The new restaurant looks good. However, it seems to have few customers.
22. They didn't use to know how to drive a car, but now they can drive well.
23. We planned to visit Petronas in the afternoon. However, we couldn't afford the fee.
24. Despite being sick, Marry didn't leave the meeting until it ended.
25. There used to be less vehicles on the roads in the past.
Đúng 1
Bình luận (0)
giải dùm em mấy câu này vs ạ nãy em ghi còn thiếu
em cảm ơn mn nhiều giải thích rọ dùm em luôn vs ạ


3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
Đúng 3
Bình luận (1)
Câu 2 đề thiếu yêu cầu
Câu 9:
Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;0\right)\) và \(\left(2;+\infty\right)\)
\(\Rightarrow\) A đúng do \(\left(-1;0\right)\subset\left(-\infty;0\right)\)
Đúng 2
Bình luận (0)
Mọi người ơi giúp em trả lời mấy câu này vs ạ ..em cảm ơn ạ

1, A
2, A
3, B
4, B
5, A
6, C
7, A
8, B
9, A
10, B
11, C
12, D
Đúng 0
Bình luận (0)
Chỉ em câu này với .em cảm ơn rất nhiều luôn ạ .Toán 9 anh chị giúp em
Giải giúp em bài này vs ạ
Em cảm ơn mọi người nhiều

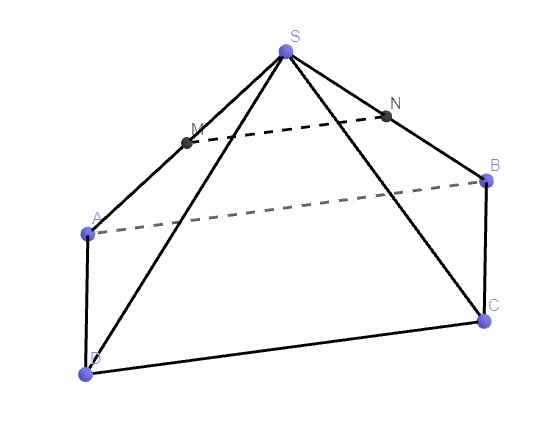
Do MN là đường trung bình tam giác ABC \(\Rightarrow MN||AB\) mà \(AB||CD\Rightarrow MN||CD\)
MN và (ABCD) không có điểm chung \(\Rightarrow MN||\left(ABCD\right)\)
MN và (SCD) không có điểm chung \(\Rightarrow MN||\left(SCD\right)\)
MN nằm trên (SAB) nên MN không song song (SAB)
Vậy MN song song với cả (ABCD) và (SCD)
Đúng 1
Bình luận (1)
Mn làm ơn giúp em bài này vs ạ ! Em đg cần rất gấp ạ ! Em cảm ơn nhiều ạ 
giúp em câu này vs ạ. em cảm ơn 
a ) H2SO4 + 2NaOH ----------> Na2SO4 + H2O
H2SO4 + 2NaHCO3 ----------> Na2SO4 + 2H2O + 2CO2
\(n_{H_2SO_4}=0,5a\)
\(n_{NaOH}=0,2.2=0,4\left(mol\right)\)
\(n_{NaHCO_3}=\dfrac{0,42}{84}=0,005\left(mol\right)\)
Trường hợp 1: H2SO4 dư
H2SO4 + 2NaOH ----------> Na2SO4 + H2O
0,2<---------0,4
nH2SO4dư = 0,5a - 0,2 (mol)
=> \(\dfrac{1}{2}n_{H_2SO_4}=0,25a-0,1\left(mol\right)\)
H2SO4 + 2NaHCO3 ----------> Na2SO4 + 2H2O + 2CO2
\(n_{H_2SO_4\left(dư\right)}=\dfrac{1}{2}n_{NaHCO_3}=0,0025\left(mol\right)\)
=> \(0,25.a-0,1=0,0025\)
=> a=0,41 (M)
Trường hợp 2: NaOH dư
H2SO4 + 2NaOH -----> K2SO4 + 2H2O
0,5a-------->a
nNaOHdư = 0.4 - a (mol)
=> \(\dfrac{1}{2}n_{NaOH\left(dư\right)}=0,2-0,5a\left(mol\right)\)
NaHCO3 + NaOH -------> Na2CO3 + H2O
0,005-------->0,005
=> 0,2 - 0.5a = 0,005
=> a = 0,39
Đúng 1
Bình luận (0)
 gấp mn giúp em câu này vs ạ e gấp lắm mn giúp em vs em cảm ơn ạ
gấp mn giúp em câu này vs ạ e gấp lắm mn giúp em vs em cảm ơn ạ
Ai giúp em câu này với em cảm ơn nhiều.
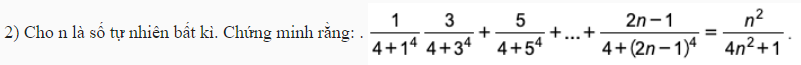
Chắc đề đúng là \(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...\)
- Với \(n=1\) đẳng thức đúng
- Giả sử đẳng thức cũng đúng với \(n=k>1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}=\dfrac{k^2}{4k^2+1}\)
- Ta cần chứng minh nó cũng đúng với \(n=k+1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\)
Thật vậy, ta có:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{4+\left(2k+1\right)^4}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(2k+1\right)^4+4\left(2k+1\right)^2+4-4\left(2k+1\right)^2}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+4k+3\right)^2-\left(4k+2\right)^2}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{k^2\left(4k^2+8k+5\right)+2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}\)
\(=\dfrac{\left(k+1\right)^2\left(4k^2+1\right)}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{\left(k+1\right)^2}{4k^2+8k+5}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\) (đpcm)
Đúng 0
Bình luận (0)