tìn giá trị nhỏ nhất lớn nhất. y=\(\sqrt{ }\)3(2-sin2x). +5
Những câu hỏi liên quan
Tìm giá trị nhỏ nhất , giá trị lớn nhất của :
y = \(\sqrt{3}\)sin2x + 2sin2x -1
\(y=\sqrt{3}sin2x-cos2x=2\left(\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x\right)=2sin\left(2x-\dfrac{\pi}{6}\right)\)
Do \(-1\le sin\left(2x-\dfrac{\pi}{6}\right)\le1\Rightarrow-2\le y\le2\)
\(y_{max}=2\) khi \(sin\left(2x-\dfrac{\pi}{6}\right)=1\)
\(y_{min}=-2\) khi \(sin\left(2x-\dfrac{\pi}{6}\right)=-1\)
Đúng 1
Bình luận (0)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:1,y5-3cosx2,y3cos^2x-2cosx+23,ycos^2x+2cos2x4,ysqrt{5-2sin^2x.cos^2x}5,ycos2x-cosleft(2x-dfrac{pi}{3}right)6,ysqrt{3}sinx-cosx-27,y2cos^2x-sin2x+58,y2sin^2x-sin2x+109,ysin^6x+cos^6x
Đọc tiếp
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
1,\(y=5-3cosx\)
2,\(y=3cos^2x-2cosx+2\)
3,\(y=cos^2x+2cos2x\)
4,\(y=\sqrt{5-2sin^2x.cos^2x}\)
5,\(y=cos2x-cos\left(2x-\dfrac{\pi}{3}\right)\)
6,\(y=\sqrt{3}sinx-cosx-2\)
7,\(y=2cos^2x-sin2x+5\)
8,\(y=2sin^2x-sin2x+10\)
9,\(y=sin^6x+cos^6x\)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y
sin
x
+
2
-
sin
2
x
A.
m
i
n
y
-
2
,
m
a
x
y
4
B.
m
i
n
y
0
,
...
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = sin x + 2 - sin 2 x
A. m i n y = - 2 , m a x y = 4
B. m i n y = 0 , m a x y = 4
C. m i n y = - 2 , m a x y = 0
D. m i n y = 0 , m a x y = 2
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số ysinx+
2
-
sin
2
x
A. B. C. D.
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=sinx+ 2 - sin 2 x
A.
B. 
C. 
D. 
Đáp án D
Do
nên
suy ra 
dấu bằng xảy ra khi và chỉ khi 
Mặt khác
nên 
Dấu bằng xảy ra khi
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất m của hàm số \(y=2\sin^2x+\sqrt{3}\sin2x\)
Lời giải:
$y=2\sin ^2x+\sqrt{3}\sin 2x=1-\cos 2x+\sqrt{3}\sin 2x$
$=1-(\cos 2x-\sqrt{3}\sin 2x)$
Áp dụng BĐT Bunhiacopxky:
$(\cos 2x-\sqrt{3}\sin 2x)^2\leq (\cos ^22x+\sin ^22x)(1+3)=4$
$\Rightarrow \cos 2x-\sqrt{3}\sin 2x\leq 2$
$\Rightarrow y=1-(\cos 2x-\sqrt{3}\sin 2x)\geq -1$
Vậy $y_{\min}=-1$. Giá trị này đạt tại $x=\frac{5\pi}{6}+2k\pi$ hoặc $x=\frac{-\pi}{6}+2k\pi$ với $k$ nguyên bất kỳ.
Đúng 0
Bình luận (0)
Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y
1
+
2
+
sin
2
x
A . 3 B.
3
+
2
C.
3
+
3
D.
2
2
+
2
Đọc tiếp
Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 1 + 2 + sin 2 x
A . 3
B. 3 + 2
C. 3 + 3
D. 2 2 + 2
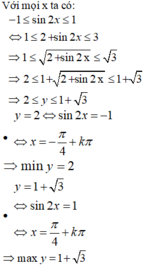
Do đó, tổng giá trị lớn nhất và nhỏ nhất của hàm số là:
Đáp án C
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
y
sin
x
+
2
-
sin
2
x
A. miny0; max y 3 B. min y 0; max y 4 C.min y 0; max y 6 D. min y 0; max y 2
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = sin x + 2 - sin 2 x
A. miny=0; max y= 3
B. min y= 0; max y= 4
C.min y= 0; max y= 6
D. min y= 0; max y = 2
Tìm tập giá tị lớn nhất, giá trị nhỏ nhất của hàm số sau y sinx +
2
-
sin
2
x
A. min y0; max y3. B. min y0; max y4. C. min y0; max y6 D. min y0; max y2.
Đọc tiếp
Tìm tập giá tị lớn nhất, giá trị nhỏ nhất của hàm số sau y = sinx + 2 - sin 2 x
A. min y=0; max y=3.
B. min y=0; max y=4.
C. min y=0; max y=6
D. min y=0; max y=2.
Tìm tập giá trị lớn nhất, giá trị nhỏ nhát của hàm số:
y
1
+
2
+
sin
2
x
Đọc tiếp
Tìm tập giá trị lớn nhất, giá trị nhỏ nhát của hàm số: y = 1 + 2 + sin 2 x
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y = sin 2 x + 4 sin x . cos x - 3 cos 2 x + 1
