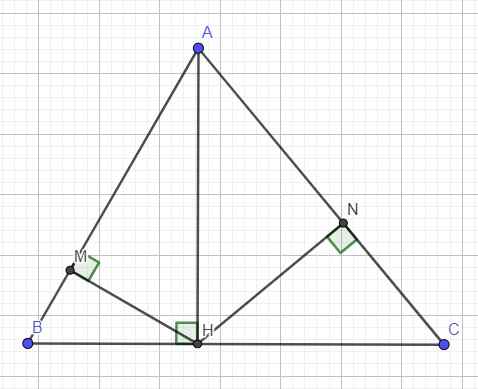
Cho ∆ABC nhọn có đường cao AH. Gọi M, N lần lượt là hình chiếu của H lên cạnh AB, AC. Chứng minh: MN = AH.sin BAC

Những câu hỏi liên quan
Cho ∆ABC nhọn (AB < AC ) có AH là đường cao. Gọi E, F lần lượt là hình chiếu của điểm H lên cạnh AB, AC
a/ Chứng minh: AE.AB = AF.AC
b/. Chứng minh: \(\Delta AEF~\Delta ACB\)
a, Xét tg ABH vuông tại H có đg cao HE
\(AE\cdot AB=AH^2\left(1\right)\)
Xét tg ACH vuông tại H có đg cao HF
\(AF\cdot AC=AH^2\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow AE\cdot AB=AF\cdot AC\)
b, Xét tg AEF và tg ACB có
\(AE\cdot AB=AF\cdot AC\Rightarrow\dfrac{AE}{AC}=\dfrac{AF}{AB}\\ \widehat{A}.chung\)
Do đó \(\Delta AEF\sim\Delta ACB\left(c.g.c\right)\)
Đúng 0
Bình luận (0)
cho tam giác ABC nhọn, đường cao AH, gọi M, N lần lượt là hình chiếu của H trên AB, AC. Chứng minh MN= AH.sinA
Câu 1. Cho tam giác ABC nhọn có đường cao AH. Gọi M và N lần lượt là hình chiếu của H lên AB và AC. Chứng minh rằng AM.AB = AN.AC.
Câu 1. Cho tam giác ABC nhọn có đường cao AH. Gọi M và N lần lượt là hình chiếu của H lên AB và AC. Chứng minh rằng AM.AB = AN.AC.
Áp dụng hệ thức lượng trong tam giác vuông ABH với đường cao BM:
\(AH^2=AM.AB\) (1)
Áp dụng hệ thức lượng trong tam giác vuông ACH với đường cao CN:
\(AH^2=AN.AC\) (2)
(1);(2)\(\Rightarrow AM.AB=AN.AC\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn (ABAC), đường cao AH. Gọi M,N,E lần lượt là trung điểm của các cạnh AB, AC và BC.a) Chứng minh rằng BMNE là hình bình hànhb) CHứng minh rằng MN là đường trung trực của AH và tứ giác MNHE là hình thang cânc) Gọi I là giao điểm của MN với A,F là hình chiếu của N lên BC, K là hình chiếu của H lên AC. CHứng minh rằng IF vuông góc với HK.các bạn giải chi tiết giúp mình nhe
Đọc tiếp
Cho tam giác ABC có 3 góc nhọn (AB>AC), đường cao AH. Gọi M,N,E lần lượt là trung điểm của các cạnh AB, AC và BC.
a) Chứng minh rằng BMNE là hình bình hành
b) CHứng minh rằng MN là đường trung trực của AH và tứ giác MNHE là hình thang cân
c) Gọi I là giao điểm của MN với A,F là hình chiếu của N lên BC, K là hình chiếu của H lên AC. CHứng minh rằng IF vuông góc với HK.
các bạn giải chi tiết giúp mình nhe
a: Xét ΔABC có
M là trung điểm của BA
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC và MN=BC/2
=>MN=BE và MN//BE
=>BMNE là hình bình hành
b: Ta có: ΔAHB vuông tại H
mà HM là đường trung tuyến
nên HM=AM
=>M nằm trên đường trung trực của AH(1)
Ta có: ΔAHC vuông tại H
mà HN là đường trung tuyến
nên HN=AC/2=AN
=>N nằm trên đường trung trực của AH(2)
Từ (1) và (2) suy ra MN là đường trung trực của AH
Xét ΔABC có
M là trung điểm của AB
E là trung điểm của BC
Do đó: ME là đường trung bình
=>ME=AC/2
mà HN=AC/2
nên ME=HN
Xét tứ giác MNEH có MN//EH
nên MNEH là hình thang
mà ME=NH
nên MNEH là hình thang cân
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, đường cao AH. Gọi M, N lần lượt là hình chiếu của H trên AB, AC. Chứng minh:Cho tam giác ABC nhọn, đường cao AH. Gọi M, N lần lượt là hình chiếu của H trên AB, AC. Chứng minh: SAMN = sin2B.sin2C.SABC
cho △ nhọn ABC, kẻ đường cao AH, gọi M và N lần lượt là hình chiếu của điểm H lên cạch AB, AC. Chứng minh
a)AM.AB=AN.AC
b)Gọi I là trung điểm của AH. Tìm điều kiện của △ABC để M,I,N thẳng hàng
a: ΔAHB vuông tại H
mà HM là đường cao
nên AM*AB=AH^2
ΔAHC vuông tại H
mà HN là đường cao
nên AN*AC=AH^2
=>AM*AB=AN*AC
b: Vì góc AMH=góc ANH=90 độ
nên A,M,H,N cùng thuộc đường tròn đường kính AH
=>I là tâm đường tròn ngoại tiếp tứ giác AMHN
Để M,I,N thẳng hàng thì MN là đường kính của (O)
=>ΔABC vuông tại A
Đúng 2
Bình luận (1)
Cho tam giác ABC có ba góc nhọn, biết
A
B
15
c
m
,
A
C
13
c
m
và đường cao
A
H
12
c
m
.
Gọi N, M lần lượt là hình chiếu vuông góc của H xuống AC và AB.a) Chứng minh rằng ΔAHN ∼ ΔACHb) Tính độ dài BCc) Chứng minh ΔAMN ∼ ΔACBd) Tính MN
Đọc tiếp
Cho tam giác ABC có ba góc nhọn, biết A B = 15 c m , A C = 13 c m và đường cao A H = 12 c m . Gọi N, M lần lượt là hình chiếu vuông góc của H xuống AC và AB.
a) Chứng minh rằng ΔAHN ∼ ΔACH
b) Tính độ dài BC
c) Chứng minh ΔAMN ∼ ΔACB
d) Tính MN
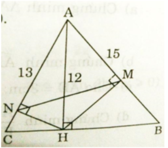
a) Xét ΔANH và ΔAHC có:
∠(NAH) chung
∠(ANH) = ∠(AHN) = 90o
⇒ ΔANH ∼ ΔAHC (g.g)
b) Ta có :
![]()
![]()
Tương tự : CH = 5 (cm)
⇒ BC = BH + CH = 9 + 5 = 14 (cm)
c) Theo chứng minh trên ta có:
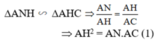
Chứng minh tương tự ta có :
ΔAMH ∼ ΔAHB ⇒ AH2 = AM.AB (2)
Từ (1) và (2) ⇒ AN.AC = AM.AB (3)
Xét ΔAMN và ΔACB có :
∠A chung
AN.AC = AM.AB
⇒ ΔAMN ∼ ΔACB (c.g.c)
d) Ta có : ΔAMH ∼ ΔAHB
![]()
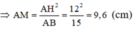
Lại có ΔAMN ∼ ΔACB (cmt)
![]()
![]()
Đúng 0
Bình luận (0)
: Cho ABC nhọn (AB<AC) có đường cao AH. Gọi M, N, P lần lượt là trung điểm của các cạnh AB,
AC, BC.
a) Chứng minh MN // HP.
b) Chứng minh
HN=1/2 AC
. Suy ra HN = MP.
c) Chứng minh MNPH là hình thang cân.
a: Xét ΔABC có
M là trung điểm cùa AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: MN//BC
hay MN//HP
Đúng 0
Bình luận (0)