Cho hai đường thẳng MN & PQ cắt nhau tại O sao cho góc MOP bằng 70 độ
a/ Tính các góc còn lại trong hình vẽ
b/ Vẽ tia Ot là tia phân giác của góc MOQ, Vẽ tia Ot' là tia đối của tia Ot. Tia Ot' là tia phân giác của góc nào? vì sao
Những câu hỏi liên quan
Vẽ hình theo diễn đạt sau đây: Hai đường thẳng mn và pq không cho điển chung. Đường thẳng xy cắt đường thẳng mn tại điểm U và cắt đường thẳng pq tại điểm V. Biết rằng: ∠(V1 ) và ∠(U1 ) là hai góc trong cùng phía; ∠(U2 ) và ∠(V1 ) là hai góc đồng vị; ∠(V2 ) và ∠(U1 ) là hai góc so le trong
Đọc tiếp
Vẽ hình theo diễn đạt sau đây: Hai đường thẳng mn và pq không cho điển chung. Đường thẳng xy cắt đường thẳng mn tại điểm U và cắt đường thẳng pq tại điểm V. Biết rằng: ∠(V1 ) và ∠(U1 ) là hai góc trong cùng phía; ∠(U2 ) và ∠(V1 ) là hai góc đồng vị; ∠(V2 ) và ∠(U1 ) là hai góc so le trong
25 tháng 3 2022 lúc 21:47
Cho ba điểm M, N, P thẳng hàng.
a) Điểm P có thuộc đường thẳng MN không? Vì sao?
b) Vẽ đường thẳng d đi qua điểm P nhưng không đi qua hai điểm M và N. Đường thẳng d có song song với đường thẳng MN không? Vì sao?
a) -Điểm P thuộc đường thẳng MN vì 3 điểm M,N,P thẳng hàng.
b) -Đường thẳng d không thể song song với đường thẳng MN. Vì d cắt MN tại P, mà đg thẳng song song thì không cắt nhau.
Đúng 2
Bình luận (0)
a) Ko thẳng hàng vì theo thứ tự điểm P nằm ngoài M,N
b)
Đường thẳng d ko song song với đường thẳng MN vì M,N,P thẳng hàng mà d cắt ngang tại P
Đúng 1
Bình luận (0)
Cho ba điểm M, N, P không thẳng hàng.a) Vẽ đoạn thẳng MN, đường thẳng MP, tia NP.b) Vẽ đường thẳng a cắt hai đoạn thẳng MN và MP nhưng không cắt đoạn tia NP.c) Gọi E là điểm chung của đường thẳng a và đoạn thẳng MN. Qua điểm E vẽ đường thẳng b cắt đoạn thẳng MP và cắt tia NP nhưng không cắt đoạn thẳng NP.
Đọc tiếp
Cho ba điểm M, N, P không thẳng hàng.
a) Vẽ đoạn thẳng MN, đường thẳng MP, tia NP.
b) Vẽ đường thẳng a cắt hai đoạn thẳng MN và MP nhưng không cắt đoạn tia NP.
c) Gọi E là điểm chung của đường thẳng a và đoạn thẳng MN. Qua điểm E vẽ đường thẳng b cắt đoạn thẳng MP và cắt tia NP nhưng không cắt đoạn thẳng NP.
Cho ba điểm M, N, P không thẳng hàng.
a) Vẽ đoạn thẳng MN, đường thẳng MP, tia NP.
b) Vẽ đường thẳng a cắt hai đoạn thẳng MN và MP nhưng không cắt đoạn tia NP.
c) Gọi E là điểm chung của đường thẳng a và đoạn thẳng MN. Qua điểm E vẽ đường thẳng b cắt đoạn thẳng MP và cắt tia NP nhưng không cắt đoạn thẳng NP.
Cho đoạn thẳng MN 6 cm. Vẽ đường tròn (M; 5cm), đường tròn này cắt MN tại E. Vẽ đường tròn (N; 3 cm), đường tròn này cắt MN tại F. Hai đường tròn tâm M và tâm N cắt nhau tại P và Q. Chứng tỏ F là trung điểm của đoạn thẳng MN.
Đọc tiếp
Cho đoạn thẳng MN = 6 cm. Vẽ đường tròn (M; 5cm), đường tròn này cắt MN tại E. Vẽ đường tròn (N; 3 cm), đường tròn này cắt MN tại F. Hai đường tròn tâm M và tâm N cắt nhau tại P và Q. Chứng tỏ F là trung điểm của đoạn thẳng MN.
F là trung điểm của đoạn thẳng MN vì F nằm giữa hai điểm M và N, đồng thời MF = NF = 3cm.
Đúng 0
Bình luận (0)
Cho hai điểm A(6;0) , B(0;8).
a. Viết phương trình đường tròn (C) đường kính AB.
b. Viết phương trình đường thẳng đi qua điểm O cắt đường tròn (C) tại hai điểm MN sao cho MN=8
Giúp mình với ạ!!!!
a: Tọa độ tâm là:
x=(6+0)/2=3 và y=(0+8)/2=4
\(IA=\sqrt{\left(3-6\right)^2+\left(4-0\right)^2}=5\)
=>(C): (x-3)^2+(y-4)^2=25
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai đường thẳng
∆
1
:
x
-
4
3
y
-
1
-
1
z
+
5
-
2
và
∆
2...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng ∆ 1 : x - 4 3 = y - 1 - 1 = z + 5 - 2 và ∆ 2 : x - 2 1 = y + 3 3 = z 1 . Giả sử M ∈ ∆ 1 , N ∈ ∆ 2 sao cho MN là đoạn vuông góc chung của hai đường thẳng ∆ 1 và ∆ 2 . Tính M N → .
A. M N → ( 5 ; - 5 ; 10 )
B. M N → ( 2 ; - 2 ; 4 )
C. M N → ( 3 ; - 3 ; 6 )
D. M N → ( 1 ; - 1 ; 2 )
Đáp án B
Gọi M 4 + 3 t ; 1 - t ; - 5 - 2 t và N 2 + u ; - 3 + 3 u ; u suy ra M N ¯ = - 2 + u - 3 t ; - 4 + 3 u + t ; u + 2 t + 5
Mặt khác M N → ⊥ u ∆ 1 → M N → ⊥ u ∆ 2 → ⇔ 3 - 2 + u - 3 t + 4 - 3 u - t - 2 u - 4 t - 10 - 2 + u - 3 t - 12 + 9 u + 3 t + u + 2 t + 5 = 0 ⇔ - 2 u - 14 t = 12 11 u + 2 t = 9 ⇔ u = 1 t = - 1
Suy ra M N → ( 2 ; - 2 ; 4 ) .
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai đường thẳng
Δ
1
:
x
-
4
3
y
-
1
-
2
z
+
5
-
1
và
Δ
2...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng Δ 1 : x - 4 3 = y - 1 - 2 = z + 5 - 1 và Δ 2 : x - 2 1 = y + 3 3 = z 1 . Giả sử M ∈ Δ 1 , N ∈ Δ 2 sao cho MN là đoạn vuông góc chung của hai đường thẳng ∆ 1 và ∆ 2 . Tính M N →
A. M N → 5 ; - 5 ; 10
B. M N → 2 ; - 2 ; 4
C. M N → 3 ; - 3 ; 6
D. M N → 1 ; - 1 ; 2
Trong không gian Oxyz, cho hai đường thẳng
∆
1
:
x
-
4
3
y
-
1
-
2
z
+
5...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng ∆ 1 : x - 4 3 = y - 1 - 2 = z + 5 - 1 và ∆ 2 : x - 2 1 = y + 3 3 = z 1 . Giả sử M ∈ ∆ 1 , N ∈ ∆ 2 sao cho MN là đoạn vuông góc chung của hai đường thẳng ∆ 1 và ∆ 2 . Tính M N →
A. M N → = ( 5 ; - 5 ; 10 )
B. M N → = ( 2 ; - 2 ; 4 )
C. M N → = ( 3 ; - 3 ; 6 )
D. M N → = ( 1 ; - 1 ; 2 )
Cho tam giác ABC. Vẽ đoạn thẳng MN. Hỏi rằng hai đường thẳng MN và BC có song song với nhau không? Vì sao?
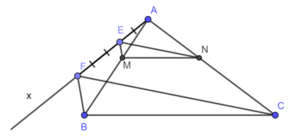
* Cách vẽ:
- Kẻ tỉa Ax bất kì khác tia AB, AC
- Trên tia Ax, lấy hai điểm E và F sao cho AE = 2 (đơn vị dài), EF = 3 (đơn vị dài)
- Kẻ đường thẳng FB
- Từ E kẻ đường thẳng song song với FB Cắt AB tại M.
- Kẻ đường thẳng FC.
- Từ E kẻ đường thẳng song song với FC cắt AC tại N.
Ta có M, N là hai điểm cần vẽ.
* Chứng minh:
Trong △ ABC, ta có:
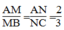
Suy ra: MN // BC (Theo định lí đảo của định lí Ta-lét)
Đúng 0
Bình luận (0)