1: Đặt góc A=a; góc B=b; góc C=c; góc D=d

Theo đề, ta có: a/1=b/2=c/3=d/4 và a+b+c+d=360

Áp dụng tính chất của DTSBN, ta được:

a/1=b/2=c/3=d/4=(a+b+c+d)/(1+2+3+4)=360/10=36

=>a=36; b=72; c=108; d=144

2:

góc C+góc D=360-130-105=230-105=125

góc C-góc D=25 độ

=>góc C=(125+25)/2=75 độ và góc D=75-25=50 độ

3:

góc B=360-57-110-75=118 độ

số đo góc ngoài tại B là:

180-118=62 độ

a) Ta thấy : A + B + C + D = 360°

Tự áp dụng tính chất dãy tỉ số bằng nhau ta có : 

A = 144° 

B = 108° 

C = 72° 

D = 36° 

b) Vì DE , CE là phân giác ADC và ACD 

=> EDC = ADE = 18° 

=> BCE = ECD = 36° 

Xét ∆DEC ta có : 

EDC + DEC + ECD = 180° 

=> DEC = 126° 

Ta có : góc ngoài tại đỉnh C

=> 180° -  BCD = 108° 

Góc ngoài tại đỉnh D 

=> 180° - ADC = 144° 

Mà DF , CF là phân giác ngoài góc C , D 

=> CDF = 72° 

=> DCF = 54° 

Xét ∆CDF ta có : 

CDF + DFC + DCF = 180° 

=> DFC = 44° 

a) Vì AB//CD, ta có góc ACD = góc BCD = 180 - góc D = 180 - 60 = 120 độ.

Vì AB//CD, ta có góc ACD = góc BAD.

Vậy số đo góc A là 120 độ.

b) Gọi góc BCD là x độ.

Theo giả thiết, góc B phần góc D = 4/5, ta có:

góc B = (4/5) * góc D

= (4/5) * 60

= 48 độ.

Vì AB//CD, ta có góc BCD = góc BAD.

Vậy góc BAD = góc BCD = x độ.

Vì tứ giác ABCD là tứ giác lồi, tổng các góc trong tứ giác ABCD là 360 độ.

Ta có: góc A + góc B + góc C + góc D = 360 độ.

Vì góc D = 60 độ, góc A = 120 độ và góc B = 48 độ, ta có:

120 + 48 + góc C + 60 = 360

góc C = 360 - 120 - 48 - 60 = 132 độ.

Vậy số đo góc B là 48 độ và số đo góc C là 132 độ.

* Ib = bài 4

Có tổng ba góc của tứ giác là 360 độ.

=> A + B + C + D = 360 độ

\(\Rightarrow\frac{A}{2}=\frac{B}{3}=\frac{C}{5}=\frac{D}{8}\)

Áp dụng tính chất của dãy tỉ số bằng nhau:

\(\frac{A}{2}=\frac{B}{3}=\frac{C}{5}=\frac{D}{8}=\frac{A+B+C+D}{2+3+5+8}=\frac{360}{18}=20\)

Có: \(\frac{A}{2}=20\Rightarrow A=40^o\)

\(\frac{B}{3}=20\Rightarrow B=60^o\)

\(\frac{C}{5}=20\Rightarrow C=100^o\)

\(\frac{D}{8}=20\Rightarrow D=160^o\)

Ta có : góc A + góc B + góc C + góc D = 360^o

Mà góc A : góc B : góc C : góc D = 2 : 3 : 5 : 8

\(=>\frac{\widehat{A}}{2}=\frac{\widehat{B}}{3}=\frac{\widehat{C}}{5}=\frac{\widehat{D}}{8}=\frac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{2+3+5+8}=\frac{360^o}{18}=20^o\)

=> góc A = 20 độ . 2 = 40 độ

góc B = 20 độ . 3 = 60 độ

góc C = 20 độ . 5 = 100 độ

góc D = 20 độ . 8 = 160 độ

\(\frac{A}{2}=\frac{B}{3}=\frac{C}{5}=\frac{D}{8}\)

\(=\frac{A+B+C+D}{2+3+5+8}=\frac{360}{18}=20\)

\(\Rightarrow\)A = 20.2 = 40 độ

B = 20 . 3 = 60 độ 

C = 20 . 5 = 100 độ

D = 20 . 8 = 160 độ

Vậy ......................

\(4{3\)

Theo bài ra, ta có:

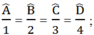  ∠ A+  ∠ B+  ∠ C+  ∠ D= 360 0  (tổng các góc của tứ giác)

Theo tính chất của dãy tỉ số bằng nhau, ta có:

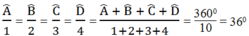
Vậy:  ∠ A= 1. 36 0  =  36 0              ∠ B= 2. 36 0 =  72 0

       ∠ C= 3. 36 0  =  108 0  ;             ∠ D= 4. 36 0  =  144 0

THeo bài ra ta có:

 A : B  : C : D = 1:2:3:4 =>\(\frac{A}{1}=\frac{B}{2}=\frac{C}{3}=\frac{D}{4}\) VÀ A + B +C + D = 360 ĐỘ ( VÌ TỔNG 4 GÓC CỦA TỨ GIÁC BẰNG 360 ĐỘ)

THeo dãy tỉ số bằng nhau :

                        \(\frac{A}{1}=\frac{B}{2}=\frac{C}{3}=\frac{D}{4}=\frac{A+B+C+D}{1+2+2+4}=\frac{360}{10}=36\)

=> A = 36.1 = 36 ĐỘ

=> B = 36.2 = 72 ĐỘ

=>C = 36.3 = 108 ĐỘ

=> D = 36.4  = 144 ĐỘ

Bài 1) 

Ta có : A + B + C + D = 360 độ

=> A + B = 140 độ

Ta có :

A = \(\frac{140+40}{2}\)= 90 độ

=> B = 90 - 40 = 50 độ

Bài 1 :

Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)

\(\Rightarrow\widehat{A}+\widehat{B}+120^o+100^o=360^o\)

\(\Rightarrow\widehat{A}+\widehat{B}+220^o=360^o\)

\(\Rightarrow\widehat{A}+\widehat{B}=140^o\)

Mà : \(\widehat{A}-\widehat{B}=40^o\)

\(\Rightarrow\widehat{A}+\widehat{A}+\widehat{B}-\widehat{B}=140^o+40^o\)

\(\Rightarrow2\widehat{A}=180^o\Leftrightarrow\widehat{A}=90^o\)

\(\Leftrightarrow\widehat{B}=140^o-\widehat{A}=140^o-90^o=50^o\)

\(KL:\widehat{A}=90^o;\widehat{B}=50^o\)

Bài 2) 

Ta có M : N : P : Q = 1 : 3 : 4 : 7 

=> M = N/3 = P/4 =Q/7 

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

=> M + N+ P + Q /1 +3+4+7 = \(\frac{360}{15}\)=24

=> M = 24 độ

N = 72 độ

P = 96 độ

Q = 168 độ

Bài 1)

a) Vì A: B:C:D = 1:2:3:4

=> A= B/2 = C/3=D/4

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

A = 36 độ

B= 72 độ

C=108 độ

D= 144 độ

b) Ta có :

A + D = 36 + 144 = 180 độ(1)

B+C = 72 + 108 = 180 độ(2)

Từ (1) và (2) ta có:

=> AB //CD (dpcm)

c) Ta có :

CDE + ADC = 180 độ(kề bù) 

=> CDE = 180 - 144 = 36

Ta có :

BCD + DCE = 180 độ ( kề bù) 

=> DCE = 180 - 108 = 72 

Xét ∆CDE ta có :

CDE + DCE + DEC = 180 (  tổng 3 góc trong ∆)

=> DEC = 180 - 72 - 36 = 72 độ 

Bài 2) 

a) Ta có ABCD có : 

A + B + C + D = 360 độ

Mà C = 80 độ

D= 70 độ

=> A+ B = 360 - 80 - 70 = 210 độ

Ta có AI là pg  góc A 

BI là pg góc B 

=> DAI = BAI = A/2 

=> ABI = CBI = B/2

=> BAI + ABI = A + B /2 

=> BAI + ABI = 210/2 = 105

Xét ∆IAB ta có :

IAB + ABI + AIB = 180 độ

=> AIB = 180 - 105

=> AIB = 75 độ

=> 

baif1: CDE và ADC như nhau mà

4: Sửa đề: DA=DC

a: BA=BC

DA=DC

=>BD là trung trực của AC

b: góc A+góc C=360-120-80=160 độ

Xét ΔBAD và ΔBCD có

BA=BD

AD=CD

BD chung

=>ΔBAD=ΔBCD

=>góc BAD=góc BCD=160/2=80 độ

3: Nếu bốn góc trong tứ giác đều là góc nhọn thì chắc chắn tổng 4 góc cộng lại sẽ nhỏ hơn 360 độ

=>Trái với  định lí tổng 4 góc trong một tứ giác

Nếu bốn góc trong tứ giác đều là góc tù thì chắc chắn tổng 4 góc cộng lại sẽ lớn hơn 360 độ

=>Trái với định lí tổng 4 góc trong một tứ giác

Do đó: 4 góc trong 1 tứ giác không thể đều là góc nhọn hay đều là góc tù được