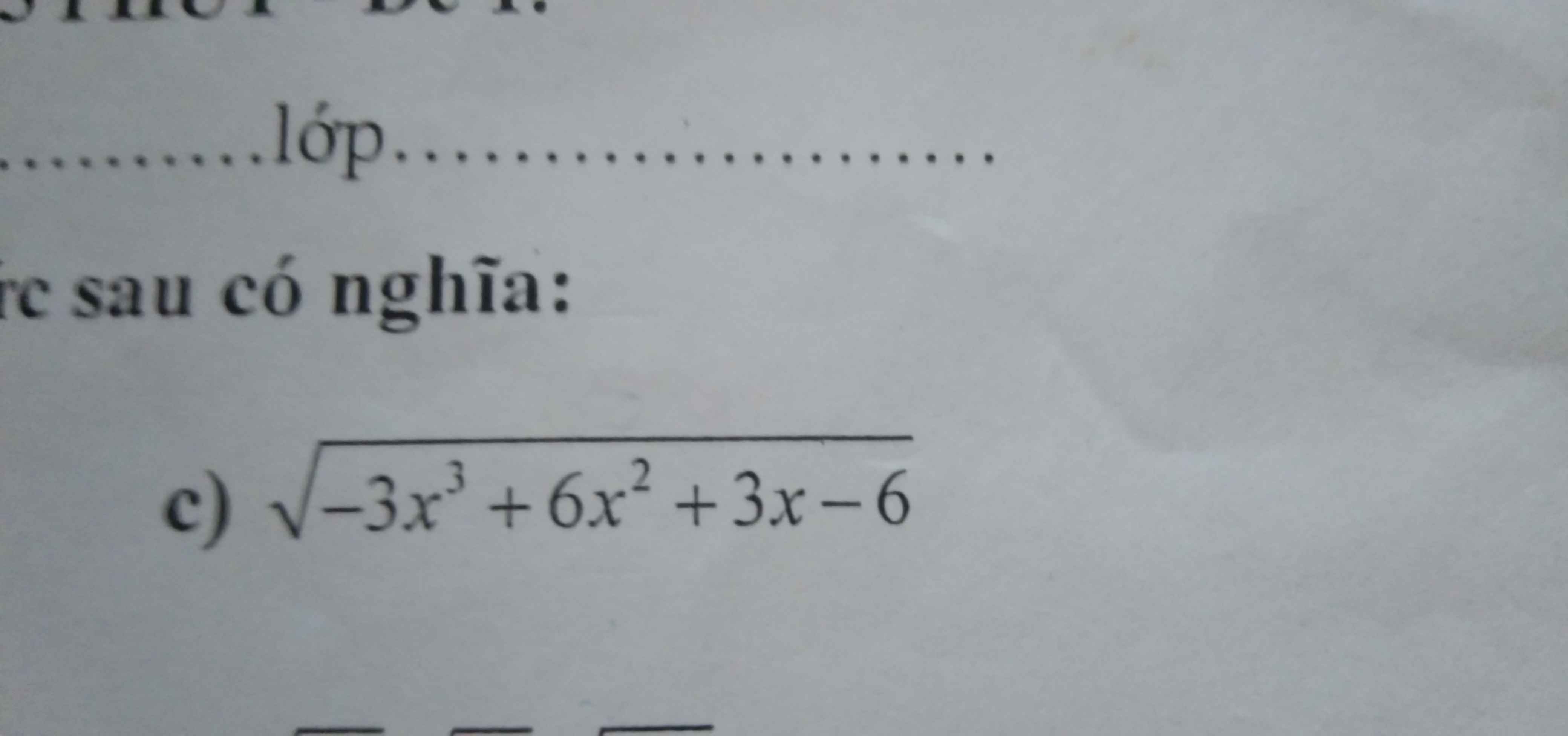
Bài toán cho không phù hợp với bậc học, vì để giải BPT bậc cao thì phải lớp 10 mới học:

ĐKXĐ:

\(-3x^3+6x^2+3x-6\ge0\)

\(\Leftrightarrow-3x^2\left(x-2\right)+3\left(x-2\right)\ge0\)

\(\Leftrightarrow\left(-3x^2+3\right)\left(x-2\right)\ge0\)

\(\Leftrightarrow3\left(1-x\right)\left(1+x\right)\left(x-2\right)\ge0\)

Trục xét dấu:

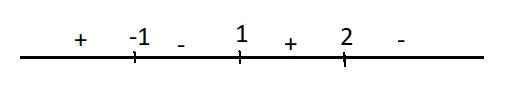
Từ đó ta thấy biểu thức có nghĩa khi: \(\left[{}\begin{matrix}x\le-1\\1\le x\le2\end{matrix}\right.\)

Chọn C.

Biểu thức có nghĩa khi và chỉ khi:

x 2  - 16 ≥ 0 ⇔  x 2   ≥   4 2  ⇔ |x|  ≥  4

Biểu thức có nghĩa khi và chỉ khi:

x - 5 ≠ 0 1 x - 5 ≥ 0 ⇔ x - 5 ≠ 0 x - 5 ≥ 0 ⇔ x ≠ 5 x ≥ 5 ⇔ x > 5

Biểu thức có nghĩa khi và chỉ khi:

4 - 2x  ≥  0 ⇔ 2x ≤ 4 ⇔ x  ≤  2

Biểu thức có nghĩa khi và chỉ khi:

x - 2 ≠ 0 x - 2 ≥ 0 ⇔ x ≠ 2 x ≥ 2 ⇔ x > 2

để căn có nghĩa thì \(2x^2+4x+5\ge0\)

\(\Rightarrow2x^2+4x+2+3\ge0\Rightarrow2\left(x+1\right)^2+3\ge0\) (luôn đúng)

\(\Rightarrow\) căn luôn có nghĩa với mọi \(x\in R\)

ĐKXĐ: \(x\in R\)

\(\sqrt{\dfrac{1}{-1+x}}=\sqrt{\dfrac{1}{x-1}}\) có nghĩa khi:

\(\left\{{}\begin{matrix}\dfrac{1}{x-1}\ge0\\x-1\ne0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x-1\ge0\\x\ne1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x\ne1\end{matrix}\right.\)

\(\Leftrightarrow x>1\)

\(ĐKXĐ:\dfrac{1}{-1+1x}>0\Leftrightarrow-1+1x< 0\\ \Leftrightarrow x< -1\)

giúp mình vs

\(\Leftrightarrow3x-2\ge0\)

hay \(x\ge\dfrac{2}{3}\)