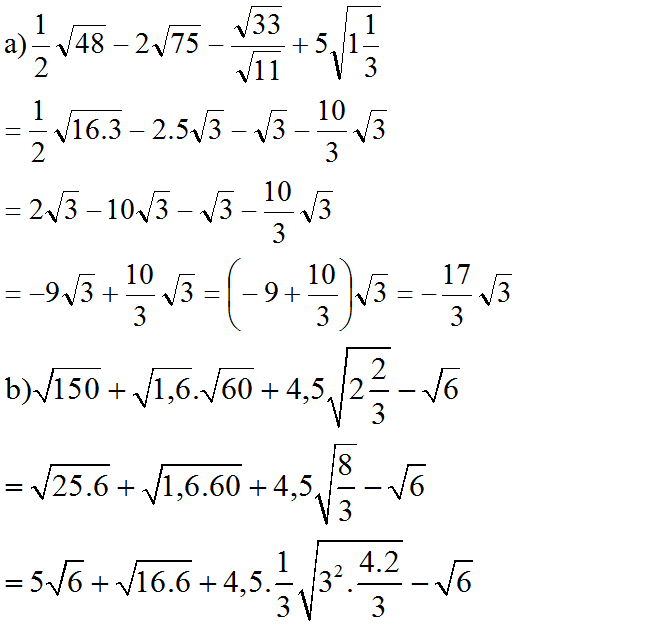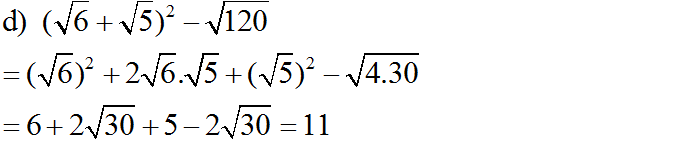a) \(\left(\sqrt{28}-2\sqrt{3}+\sqrt{7}\right)\sqrt{7}+\sqrt{84}\)

\(=\left(2\sqrt{7}-2\sqrt{3}+\sqrt{7}\right)\sqrt{7}+2\sqrt{21}\)

\(=\left(3\sqrt{7}-2\sqrt{3}\right)\sqrt{7}+2\sqrt{21}\)

\(=21-2\sqrt{21}+2\sqrt{21}\)

\(=21\)

b) \(\dfrac{\sqrt{4-2\sqrt{3}}}{\sqrt{6}-\sqrt{2}}\)

\(=\dfrac{\sqrt{\left(\sqrt{3}\right)^2-2\sqrt{3}\cdot1+1^2}}{\sqrt{6}-\sqrt{2}}\)

\(=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{6}-\sqrt{2}}\)

\(=\dfrac{\left|\sqrt{3}-1\right|}{\sqrt{2}\left(\sqrt{3}-1\right)}\)

\(=\dfrac{\sqrt{3}-1}{\sqrt{2}\left(\sqrt{3}-1\right)}\)

\(=\dfrac{1}{\sqrt{2}}\)

2\(\left(\sqrt{28}-2\sqrt{3}+\sqrt{7}\right)\sqrt{7}+\sqrt{84}\)

= \(14-\sqrt{84}+7-\sqrt{84}\)

= 21

Câu 1 = 15

Câu 2 = 21

Nha!

K VÀ KB NHA !

1.  \(\left(3\sqrt{5}-2\sqrt{3}\right)5+\sqrt{60}\)

= \(15-\sqrt{60}+\sqrt{60}\)

= 15

a: \(=3\sqrt{2}\left(\sqrt{3}-\sqrt{2}\right)-3\sqrt{6}\)

=3căn 6-6-3căn 6=-6

b: \(=\dfrac{a+\sqrt{ab}}{\sqrt{a}-\sqrt{b}}-\sqrt{a}\)

\(=\dfrac{a+\sqrt{ab}-a+\sqrt{ab}}{\sqrt{a}-\sqrt{b}}=\dfrac{2\sqrt{ab}}{\sqrt{a}-\sqrt{b}}\)

a) \(\text{2}\sqrt{\text{18}}-9\sqrt{50}+3\sqrt{8}\)

= \(\text{6}\sqrt{\text{2}}-45\sqrt{2}+6\sqrt{2}\)

= \(-33\sqrt{2}\)

b) = \(7-2.\sqrt{7}.\sqrt{3}+3+7.2\sqrt{21}\)

= \(10-2\sqrt{21}+14\sqrt{21}\)

= \(10+12\sqrt{21}\)

a, \(\dfrac{1}{2}\sqrt{48}-2\sqrt{75}-\dfrac{\sqrt{33}}{\sqrt{11}}+5\sqrt{1\dfrac{1}{3}}\)

= \(2\sqrt{3}-10\sqrt{3}-\dfrac{\sqrt{3}\cdot\sqrt{11}}{\sqrt{11}}+5\sqrt{\dfrac{4}{3}}\)

= \(2\sqrt{3}-10\sqrt{3}-\sqrt{3}+5\sqrt{\dfrac{12}{3^2}}\)

= \(2\sqrt{3}-10\sqrt{3}-\sqrt{3}+5\dfrac{2\sqrt{3}}{3}\)

= \(2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{10\sqrt{3}}{3}\)

= \(-9\sqrt{3}+\dfrac{10\sqrt{3}}{3}=\dfrac{-27\sqrt{3}}{3}+\dfrac{10\sqrt{3}}{3}=\dfrac{-17\sqrt{3}}{3}\)

b, \(\sqrt{150}+\sqrt{1,6}\cdot\sqrt{60}+4.5\sqrt{2\dfrac{2}{3}}-\sqrt{6}\)

= \(5\sqrt{6}+\dfrac{2\sqrt{10}}{5}\cdot2\sqrt{15}+4,5\sqrt{\dfrac{8}{3}}-\sqrt{6}\)

= \(5\sqrt{6}+4\sqrt{6}+4,5\sqrt{\dfrac{24}{3^2}}-\sqrt{6}\)

= \(5\sqrt{6}+4\sqrt{6}+4,5\cdot\dfrac{2\sqrt{6}}{3}-\sqrt{6}\)

= \(5\sqrt{6}+4\sqrt{6}+3\sqrt{6}-\sqrt{6}=11\sqrt{6}\)

c, \(\left(\sqrt{28}-2\sqrt{3}+\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{84}\)

= \(\left(2\sqrt{7}-2\sqrt{3}+\sqrt{7}\right)\cdot\sqrt{7}+2\sqrt{21}\)

= \(\left(3\sqrt{7}-2\sqrt{3}\right)\cdot\sqrt{7}+2\sqrt{21}\)

= \(21-2\sqrt{21}+2\sqrt{21}=21\)

d, \(\left(\sqrt{6}+\sqrt{5}\right)^2-\sqrt{120}\)

= \(6+2\sqrt{30}+5-2\sqrt{30}=11\)

a) \(\sqrt{20}-\sqrt{45}+3\sqrt{18}+\sqrt{72}\)

= \(2\sqrt{5}-3\sqrt{5}+9\sqrt{2}+6\sqrt{2}\)

= \(-\sqrt{5}+15\sqrt{2}\)

b) \(\left(\sqrt{28}-2\sqrt{3}+\sqrt{7}\right)\sqrt{7}+\sqrt{84}\)

= \(\left(2\sqrt{7}-2\sqrt{3}+\sqrt{7}\right)\sqrt{7}+2\sqrt{21}\)

= \(2.7-2\sqrt{21}+7+2\sqrt{21}=14+7=21\)

c) \(\left(\sqrt{6}+\sqrt{5}\right)^2-\sqrt{120}\)

= \(6+2\sqrt{6}.\sqrt{5}+5-2\sqrt{30}\)

= \(11+2\sqrt{30}-2\sqrt{30}=11\)

d) \(\left(\dfrac{1}{2}-\sqrt{\dfrac{1}{2}}-\dfrac{3}{2}\sqrt{2}+\dfrac{4}{5}\sqrt{200}\right):\dfrac{1}{8}\)

= \(\left(\dfrac{1}{2}-\sqrt{\dfrac{1}{2}}-\dfrac{3}{2}\sqrt{2}+8\sqrt{2}\right).8\)

= \(4-4\sqrt{2}-12\sqrt{2}+64\sqrt{2}=4+48\sqrt{2}\)

Bài này dễ ẹc ( đâu có khó đâu :)) )

a) \(\sqrt{20}-\sqrt{45}+3\sqrt{18}+\sqrt{72}\)

\(=\sqrt{2^2.5}-\sqrt{3^2.5}+3\sqrt{3^2.2}+\sqrt{6^2.2}\)

\(=2\sqrt{5}-3\sqrt{5}+9\sqrt{2}+6\sqrt{2}\)

\(=\left(2-3\right)\sqrt{5}+\left(9+6\right)\sqrt{2}\)

\(=15\sqrt{2}-\sqrt{5}\)

b) \(\left(\sqrt{28}-2\sqrt{3}+\sqrt{7}\right)\sqrt{7}+\sqrt{84}\)

\(=\sqrt{2^2.7}.\sqrt{7}-2\sqrt{3}.\sqrt{7}+\sqrt{7}.\sqrt{7}+\sqrt{2^2.21}\)

\(=2.7-2\sqrt{21}+7+2\sqrt{21}\)

\(=14+7+\left(2-2\right)\sqrt{21}=21\)

c) \(\left(\sqrt{6}+\sqrt{5}\right)^2-\sqrt{120}\)

\(=6+2\sqrt{30}+5-\sqrt{2^2.30}\)

\(=6+5+2\sqrt{30}-2\sqrt{30}=11\)

d) \(\left(\dfrac{1}{2}\sqrt{\dfrac{1}{2}}-\dfrac{3}{2}\sqrt{2}+\dfrac{4}{5}\sqrt{200}\right):\dfrac{1}{8}\)

\(=\left(\dfrac{1}{2}\sqrt{\dfrac{2}{2^2}}-\dfrac{3}{2}\sqrt{2}+\dfrac{4}{5}\sqrt{10^2.2}\right):\dfrac{1}{8}\)

\(=\left(\dfrac{1}{4}\sqrt{2}-\dfrac{3}{2}\sqrt{2}+8\sqrt{2}\right).8\)

\(=2\sqrt{2}-12\sqrt{2}+64\sqrt{2}=54\sqrt{2}\)

Hok tốt

\(a.\sqrt{20}-\sqrt{45}+3\sqrt{18}-\sqrt{72}\)

= \(2\sqrt{5}-3\sqrt{5}+9\sqrt{2}-6\sqrt{2}=3\sqrt{2}-\sqrt{5}\)

b. \(\left(\sqrt{28}-2\sqrt{3}+\sqrt{7}\right)\sqrt{7}+\sqrt{84}\)

= \(\sqrt{196}-2\sqrt{21}+7+\sqrt{84}\)

= \(14-2\sqrt{21}+7+2\sqrt{21}=21\)

c. \(\left(\sqrt{6}+\sqrt{5}\right)^2-\sqrt{120}\)

= \(6+2\sqrt{30}+5-\sqrt{120}=6+2\sqrt{30}+5-2\sqrt{30}=11\)

d. \(\left(\dfrac{1}{2}-\sqrt{\dfrac{1}{2}}-\dfrac{3}{2}\sqrt{2}+\dfrac{4}{5}\sqrt{200}\right):\dfrac{1}{8}\)

= \(4-\dfrac{8}{\sqrt{2}}-\dfrac{3\sqrt{2}}{4}+\dfrac{32\sqrt{200}}{5}\)

= \(4-\dfrac{8}{\sqrt{2}}-\dfrac{3}{2\sqrt{2}}+\dfrac{32.5.\sqrt{8}}{5}=4-\dfrac{16}{2\sqrt{2}}+32\sqrt{8}\)

= \(\dfrac{8\sqrt{2}-16+256}{2\sqrt{2}}=\dfrac{240+8\sqrt{2}}{2\sqrt{2}}=60\sqrt{2}+4\)