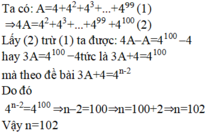Đáp án cần chọn là: D

Olm chào em, em làm như này là cưa đúng rồi, em nhé. 

D=4+4^2+...+4^n

=>\(4\cdot D=4^2+4^3+...+4^{n+1}\)

=>\(3D=4^{n+1}+4^n+...+4^3+4^2-4^n-...-4^2-4\)

=>\(3D=4^{n+1}-4\)

=>\(D=\dfrac{4^{n+1}-4}{3}\)

\(b,A=\left(1+4+4^2\right)+\left(4^3+4^4+4^5\right)+...\left(4^{57}+4^{58}+4^{59}\right)\\ A=\left(1+4+4^2\right)+4^3\left(1+4+4^2\right)+...+4^{57}\left(1+4+4^2\right)\\ A=\left(1+4+4^2\right)\left(1+4^3+...+4^{57}\right)\\ A=21\left(1+4^3+...+4^{57}\right)⋮7\)

a: \(\Leftrightarrow2x+1\in\left\{1;3\right\}\)

hay \(x\in\left\{0;1\right\}\)

Lê Quang Phúc 

bài 1:Tính nhanh

b)58+42+32nhân 8+5 nhân 16

c)(42 nhân 43+46nhân 57+43)-360:4

bài 2:tìm x

a)890:x=35 dư 15

c)1482:x+23=80

ai trả lời đầu tiên mà đúng thì mình cho nhé.

 a, 21 chia hết cho 2n + 1

=> 2n + 1 thuộc Ư(21) = {1; 3; 7; 21} (do n thuộc N)

=> 2n thuộc {0; 2; 6; 20}

=> n thuộc {0; 1; 3; 10}

b, 5n + 4 chia hết cho n

Mà n chia hết cho n => 5n chia hết cho n

=> 4 chia hết cho n

=> n thuộc Ư(4) = {1; 2; 4} (do n thuộc N)

c, 3n + 7 chia hết cho n + 1

=> 3n + 3 + 4 chia hết cho n + 1

=> 3(n + 1) + 4 chia hết cho n + 1

Mà n + 1 chia hết cho n + 1 => 3(n + 1) chia hết cho n + 1

=> 4 chia hết cho n + 1

=> n + 1 thuộc Ư(4) = {1; 2; 4} (do n thuộc N)

=> n thuộc {0; 1; 3}

Do n thuộc N => 2n thuộc N => 2n +1 thuộc N => 2n + 1 thuộc ước tự nhiên của 21

có 2n chia hết cho 2 => 2n +1 chia hết cho 3

=> 2n +1 thuộc +-21;+-3

=>n thuộc 10; -11 ;1; -2

vậy n thuộc 10; -11;1;-2

Đặt d = (4n + 3, 5n + 1). Ta có:

\(\left\{{}\begin{matrix}4n+3⋮d\\5n+1⋮d\end{matrix}\right.\Rightarrow5\left(4n+3\right)-4\left(5n+1\right)⋮d\Rightarrow\left(20n+15\right)-\left(20n+4\right)⋮d\Rightarrow11⋮d\Rightarrow d\in\left\{1;11\right\}\)

Để hai số đó không nguyên tố cùng nhau thì d \(\ne\) 1. Do đó d = 11. Muốn d = 11 thì hai số đó đều chia hết cho 11. Ta thấy:

\(\left\{{}\begin{matrix}4n+3⋮11\Rightarrow4n+3-11⋮11\Rightarrow4n-8⋮11\Rightarrow4\left(n-2\right)⋮11\Rightarrow n-2⋮11\\5n+1⋮11\Rightarrow5n+1-11⋮11\Rightarrow5n-10⋮11\Rightarrow5\left(n-2\right)⋮11\Rightarrow n-2⋮11\end{matrix}\right.\)

Vậy, để hai số đó không nguyên tố cùng nhau thì n chia cho 11 dư 2.

\(A=1+4+4^2+4^3+4^4+4^5+...+4^{2019}+4^{2020}+4^{2021}\)

\(=\left(1+4+4^2\right)+\left(4^3+4^4+4^5\right)+...+\left(4^{2019}+4^{2020}+4^{2021}\right)\)

\(=21+4^3\cdot21+...+4^{2019}\cdot21\)

\(=21\left(1+4^3+...+4^{2019}\right)⋮21\)

\(A=1+4+4^2+4^3+...+4^{2021}\\=(1+4+4^2)+(4^3+4^4+4^5)+(4^6+4^7+4^8)+...+(4^{2019}+4^{2020}+4^{2021})\\=21+4^3\cdot(1+4+4^2)+4^6\cdot(1+4+4^2)+...+4^{2019}\cdot(1+4+4^2)\\=21+4^3\cdot21+4^6\cdot21+...+4^{2019}\cdot21\\=21\cdot(1+4^3+4^6+...+4^{2019})\)

Vì \(21\cdot(1+4^3+4^6+...+4^{2019})\vdots21\)

nên \(A\vdots21\)

\(\text{#}Toru\)