Cho hình thoi ABCD có \(\widehat{A}=60^0\). Gọi O là giao điểm của hai đường chéo; E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA.
Chứng minh rằng 6 điểm E, B, F, G, D, H thuộc cùng một đường tròn ?
Cho hình thoi ABCD cạnh a có BAD=60 độ. Gọi O là giao điểm của hai đường chéo AC và BD. Gọi O là giao điểm hai đường chéo AC và BD. Gọi G là trọng tâm tam giác ABD, E là điểm đối xứng của O qua D, H là giao điểm AD và GE. Tính độ dài vector AH
Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình thoi cạnh \(a\) có \(O\) là giao điểm của hai đường chéo, \(\widehat {ABC} = {60^ \circ },SO \bot \left( {ABCD} \right),SO = a\sqrt 3 \). Tính khoảng cách từ \(O\) đến mặt phẳng \(\left( {SCD} \right)\).

Kẻ \(OI \bot C{\rm{D}}\left( {I \in C{\rm{D}}} \right),OH \bot SI\left( {H \in SI} \right)\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SO \bot \left( {ABCD} \right) \Rightarrow SO \bot C{\rm{D}}\\OI \bot C{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {SOI} \right)\\\left. \begin{array}{l} \Rightarrow C{\rm{D}} \bot OH\\OH \bot SI\end{array} \right\} \Rightarrow OH \bot \left( {SC{\rm{D}}} \right)\\ \Rightarrow d\left( {O,\left( {SC{\rm{D}}} \right)} \right) = OH\end{array}\)
\(\Delta ABC\) đều \( \Rightarrow AC = a \Rightarrow OC = \frac{1}{2}AC = \frac{a}{2}\)
\(\Delta ABD\) có \(\widehat {BA{\rm{D}}} = {120^ \circ } \Rightarrow B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2} - 2{\rm{A}}B.A{\rm{D}}} = a\sqrt 3 \Rightarrow OD = \frac{1}{2}B{\rm{D}} = \frac{{a\sqrt 3 }}{2}\)
\(\Delta OCD\) vuông tại \(O\) có đường cao \(OI\)
\( \Rightarrow OI = \frac{{OC.O{\rm{D}}}}{{C{\rm{D}}}} = \frac{{a\sqrt 3 }}{4}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OI \Rightarrow \Delta SOI\) vuông tại \(O\) có đường cao \(OH\)
\( \Rightarrow OH = \frac{{SO.OI}}{{\sqrt {S{O^2} + O{I^2}} }} = \frac{{a\sqrt {51} }}{{17}}\)
Vậy \(d\left( {O,\left( {SCD} \right)} \right) = OH = \frac{{a\sqrt {51} }}{{17}}\).
Cho hình thoi ABCD có \(\widehat{ABC}< 90^0\). Gọi O là giao điểm của 2 đường chéo AC và BD. Kẻ OH vuông góc với BC. Gọi M và N là 2 điểm lần lượt thuộc DC và DA, sao cho \(\widehat{MON}=\widehat{DAC}\). Chứng minh rằng 3 đường thẳng BM ; HN và AC đồng quy tại I
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán hỗ trợ giúp đỡ em tham khảo với ạ!
Em cám ơn nhiều lắm ạ!
Cho hình thoi ABCD có ∠ A = 60 ° . Gọi O là giao điểm của hai đường chéo; E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Chứng minh rằng sáu điểm E, B, F, G, D, H thuộc cùng một đường tròn.
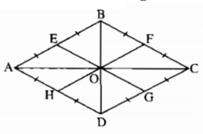
Đặt OB = OD = a. Hãy chứng minh OE = a. Tương tự, OF = OG = OH = a. Từ đó suy ra sáu điểm E, B, F, G, D, H cùng thuộc một đường tròn (O;a).
Cho hình thoi ABCD. Gọi O là giao điểm của hai đường chéo, biết AB = 5cm và AO = 3cm. Diện tích hình thoi ABCD là:
A. 12 c m 2
B. 24 c m 2
C. 36 c m 2
D. 48 c m 2
Cho hình thoi ABCD có diện tích là 40 c m 2 . Gọi O là giao điểm của hai đường chéo. Tính diện tích tam giác AOB?
A. 10 c m 2
B. 12 c m 2
C. 8 c m 2
D. 5 c m 2
Vì ABCD là hình thoi có O là giao điểm của hai đường chéo nên O là trung điểm của AC và BD.
Suy ra
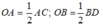
Diện tích hình thoi ABCD là:
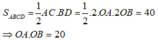
Diện tích tam giác vuông OAB là:
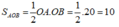
Chọn đáp án A
Cho hình thoi ABCD có diện tích là 40 c m 2 . Gọi O là giao điểm của hai đường chéo. Tính diện tích tam giác AOB?
A. 10 c m 2
B. 12 c m 2
C. 8 c m 2
D. 5 c m 2
Vì ABCD là hình thoi có O là giao điểm của hai đường chéo nên O là trung điểm của AC và BD.
Suy ra
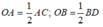
Diện tích hình thoi ABCD là:
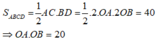
Diện tích tam giác vuông OAB là:
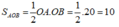
Chọn đáp án A
cho hình thoi ABCD gọi o là giao điểm hai đường chéo biết AB = 20 cm OA = 16 cm OB = 12 cm tính độ dài các cạnh và đường chéo của hình thoi
Vì ABCD là hình thoi nên \(AB=BC=CD=DA=20\left(cm\right)\)
Và AC cắt BD tại O nên O là trung điểm AC,BD
\(\Rightarrow AC=2AO=32\left(cm\right);BD=2OB=24\left(cm\right)\)
Cho hình thoi ABCD, \(\widehat{A}=90^0\), O là giao điểm hai đường chéo, vẽ OF vuông góc với AB (F\(\in\)AB).
a) Chứng minh đường tròn tâm O, bán kính OF tiếp xúc với bốn cạnh của hình thoi ABCD.
b) Đường tròn ngoại tiếp tam giác ABD cắt AC tại điểm thứ hai K. Chứng minh K là trực tâm của tam giác BCD.
c) Cho biết \(\widehat{BAD}=60^0\), cạnh AB=a
i. Tính diện tích hình thoi ABCD theo a
ii. Chứng minh rằng \(\frac{AO}{OK}=\frac{ÃC}{CK}\)