Vì ABCD là hình thoi có O là giao điểm của hai đường chéo nên O là trung điểm của AC và BD.
Suy ra
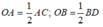
Diện tích hình thoi ABCD là:
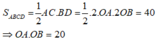
Diện tích tam giác vuông OAB là:
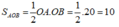
Chọn đáp án A
Vì ABCD là hình thoi có O là giao điểm của hai đường chéo nên O là trung điểm của AC và BD.
Suy ra
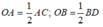
Diện tích hình thoi ABCD là:
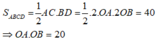
Diện tích tam giác vuông OAB là:
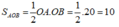
Chọn đáp án A
Cho hình thoi ABCD có diện tích là 40 c m 2 . Gọi O là giao điểm của hai đường chéo. Tính diện tích tam giác AOB?
A. 10 c m 2
B. 12 c m 2
C. 8 c m 2
D. 5 c m 2
Cho hình vuông ABCD,lấy M trên đường chéo AC . Gọi E và F lần lượt là hình chiếu của M trên AD và DC, K là giao điểm của Em với BC, H là giao điểm của BM với EF
a) c/m MKCF là hình vuông
b) tính diện tích tứ giác ABKC, biết diện tích hình vuông MKCF=16cm2 và ME/MK=1/2
c) c/m tam giác MEF=KBM. từ đó suy ra BH vuông góc với EF
d) c/m 3 đường thẳng BH,AF,CE dồng quy
Cho hv ABCD, cạnh là a, 2 đường chéo cắt nhau tại O , I thuộc AB, M thuộc BC sao cho góc IOM=90 ( I, M ko trùng với các đỉnh hình vuông).Gọi N là giao điểm AM và CD.K là giao điểm của OM và BN.
a, c/m tam giác BEO và tam giác CMO bằng nhau, và tính diện tích tứ giác BIOM
b, c/m 2 góc BKM và BCO bằng nhau
c, cm 1/CD2 =1/CM +1/AN2
1, cho tam giác abc có 2 trung tuyến bd và ce cắt nhau tại g gọi m,n là trung điểm của bg và cg
a, c/m MNDE là HBH
b, tìm d/k của abc là HCN
2, cho tam giác abc vuông tại a đường trung tuyến am, gọi I là trung điểm của ab và d là điểm đối xứng của m qua I
a, c/m ad// bm và c/m adbm là hin h thoi
b, gọi e là giao điểm của am và ad, c/m AE=EM
c, cho bc=5, ac=4 tính diện tích
3, cho tam giác abc vuông tại a , trung tuyến am , gọi I là giao điểm của AB N là điểm đối xứng với m qua I
a, c/m anmc, ambn là hình gì? tại sao?b, cho ab=4, ac=6. tính diện tích ambn
Cho hình chữ nhật ABCD có AB = 20cm, AD = 15cm a) Tính độ dài đường chéo BD b) Trên cạnh AD lấy điểm M sao cho AM = 5cm. CM cắt BD tại P và đường thẳng AB tại Q. Tính tỉ số diện tích 2 tam giác PDM và PBC c) Gọi N là trung điểm của cạnh AB. C/m: 2 tam giác AMN và DMC đồng dạng d) C/m: MA là tia phân giác của góc QMN
1. Cho hình vuông ABCD có độ dài đường chéo bằng 12 cm. M là một điểm bất kỳ trên cạnh AB, O là giao điểm hai đường chéo. Đường thẳng qua O và vuông góc với OM cắt BC tại N. Tính diện tích tứ giác OMBN? .
2. Cho tam giác ABC có diện tích 12cm^2. N là trung điểm BC. M trên AC sao cho AM/AC = 1/3. AN cắt BM tại O. Khi đó diện tích của tam giác OAM là?
gọi O là giao điểm hai đường chéo AC và BD của hình thang ABCD( AB//CD). đường thẳng qua O // với AB cắt AD và BC lần lượt tại M và N
a, cm OM=ON
b, cm \(\frac{1}{AB}\)+ \(\frac{1}{CD}\)=\(\frac{2}{MN}\)
c, biết diện tích tam giác AOB = \(a^2\), dienj tích tam giác COD =\(b^2\). tính diện tích hình thang ABCD
d, nếu góc D< góc C < \(90^o\). cmr BD>AC
Cho hình bình hành ABCD .gọi O là giao điểm của 2 đường chéo và M,N lần lượt là trung điểm của AD , BC . BM và DN cắt AC lần lượt tại E và F . a/ Tứ giác BMDN là hình gì ? vì sao ? b/ Chứng minh AE = E F = FC . c/ Tính diện tích tam giác DBM .Biết diện tích Hình bình hành là 30 cm