Cho đường tròn (O) và hai điểm A, B nằm ngoài đường tròn. Dựng đường kính COD sao cho AC = BD

Những câu hỏi liên quan
Cho đường tròn (O) và hai điểm A, B nằm bên ngoài đường tròn. Dựng đường kính COD sao cho AC = BD.
* Cách dựng
- Dựng A’ đối xứng với A qua tâm O của đường tròn
- Dựng đường thẳng x là trung trực của A’B
- Gọi giao điểm của đường thẳng x và đường tròn (O) là D
- Dựng đường kính COD
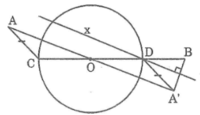
* Chứng minh
Ta có: OA = OA’ và OD = OC
Suy ra tứ giác ACA’D là hình bình hành
Suy ra: AC = A’D
Lại có: A’D = BD (tính chất đường trung trực)
Suy ra: AC = BD
Đúng 0
Bình luận (0)
Cho đường tròn (O) và hai điểm A, B nằm bên ngoài đường tròn. Dựng đường kính COD sao cho AC=BD.
Cho đường tròn tâm O và 2 điểm A,B nằm bên ngoài đường tròn dựng đường kính COD sao cho AC=BD
Cho đường tròn tâm O , bán kính R và điểm A nằm ngoài đường tròn sao cho OA > 2R . Từ A kẻ hai tiếp tuyến AB , AC đến đường tròn (O) (B,C là 2 tiếp điểm ) . Trên cung nhỏ BC lấy điểm D sao cho CD < BD , tia AD cắt đường tròn (O) tại điểm E (E khác D). Qua B vẽ đường thẳng song song với AE cắt (O) tại K , CK cắt DE tại M.Vẽ tia AC cắt BE tại F .c/m nếu E là trung điểm của BF thì BC=DE
cho đường tròn (O;R) từ điểm A ở bên ngoài đường tròn sao cho OA = 2R. Kẻ 2 tiếp tuyến AB,AC với đường tròn ( B,C tiếp điểm)
a) vẽ đường kính COD. C/Minh BD//AO
b) gọi E là 1 điểm thuộc cung nhỏ BC. kẻ tiếp tuyến với đường tròn tại E cắt AB và AC theo thức tự M,N. TÍNH GÓC MON VÀ chu vi tam giác AMN
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn. Từ A kẻ các đường AB, AC lần lượt vuông góc với OB, OC (B,C thuộc đường tròn). Vẽ đường kính BD của đường trên (O), AD cắt (O) tại E. Gọi H là giao điểm của OA và BC.
a. Chứng minh: A, B, O, C cùng thuộc một đường tròn
b. Chứng minh: CD 2OH
Đọc tiếp
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn. Từ A kẻ các đường AB, AC lần lượt vuông góc với OB, OC (B,C thuộc đường tròn). Vẽ đường kính BD của đường trên (O), AD cắt (O) tại E. Gọi H là giao điểm của OA và BC.
a. Chứng minh: A, B, O, C cùng thuộc một đường tròn
b. Chứng minh: CD = 2OH
a. Chứng minh: A, B, O, C cùng thuộc một đường tròn
b. Chứng minh: CD = 2OH
Bài 4: Cho đường tròn (O) và một điểm A nằm ngoài đường tròn. Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Vẽ đường kính BD của đường tròn (O) a) Chứng minh: OA BC và DC // OA. b) Đường thẳng AD cắt (O) tại điểm thứ hai là E. Chứng minh: AE.AD = AC2
a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA⊥BC
Đúng 1
Bình luận (0)
Cho đường tròn (O,R) điểm A nằm bên ngoài đường tròn, vẽ hai tiếp tuyến AB,AC với đường tròn (B và C là hai tiếp điểm) vẽ đường kính CD của đường tròn O. Chứng minh :
a)OA vuông góc BC
b)BD // OA
c)Cho R =6cm, AB =8cm. Tính BC.
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn. Từ A vẽ hai tiếp tuyển AB, AC của đường tròn (O) với B và C là hai tiếp điểm. Vẽ đường kính BD của đường tròn (O), AD cắt đường tròn (0) tại E. Gọi H là giao điểm của OA và BC, K là trung điểm ED. a/ Chứng minh A, B, O, K, C nằm trên đường tròn b/ Chứng minh AE. AD AC.AC c/ Vẽ OK cắt BC tại F. Chứng minh FD là tiếp tuyển của đường tròn (O).
Đọc tiếp
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn. Từ A vẽ hai tiếp tuyển AB, AC của đường tròn (O) với B và C là hai tiếp điểm. Vẽ đường kính BD của đường tròn (O), AD cắt đường tròn (0) tại E. Gọi H là giao điểm của OA và BC, K là trung điểm ED. a/ Chứng minh A, B, O, K, C nằm trên đường tròn b/ Chứng minh AE. AD= AC.AC c/ Vẽ OK cắt BC tại F. Chứng minh FD là tiếp tuyển của đường tròn (O).
a: ΔODE cân tại O
mà OK là trung tuyến
nên OK vuông góc DE
góc OKA=góc OBA=góc OCA=90 độ
=>O,K,C,A,B cùng thuộc 1 đường tròn
b: Xét ΔACE và ΔADC có
góc ACE=góc ADC
góc CAE chung
=>ΔACE đồng dạng với ΔADC
=>AC/AD=AE/AC
=>AC^2=AD*AE
c: Xét ΔOKA vuông tại K và ΔOHF vuông tại H có
góc O chung
=>ΔOKA đồng dạng với ΔOHF
=>OK/OH=OA/OF
=>OK*OF=OH*OA=OE^2=OD^2
=>FD là tiếp tuyến của (O)
Đúng 1
Bình luận (0)













